早教吧作业答案频道 -->数学-->
从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数y=kx+b的系数k、b,则一次函数y=kx+b的图象不经过第三象限的概率是.
题目详情
从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数y=kx+b的系数k、b,则一次函数y=kx+b的图象不经过第三象限的概率是___.
▼优质解答
答案和解析
画树状图为:
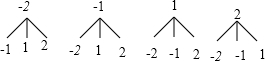
共有12种等可能的结果数,其中一次函数y=kx+b的图象不经过第三象限的结果数为4,
所以一次函数y=kx+b的图象不经过第三象限的概率=
=
.
故答案为
.

共有12种等可能的结果数,其中一次函数y=kx+b的图象不经过第三象限的结果数为4,
所以一次函数y=kx+b的图象不经过第三象限的概率=
| 4 |
| 12 |
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
看了 从-2,-1,1,2这四个数...的网友还看了以下:
用12345五个数安排成个五位数,求排出数是15的倍数概率 2020-05-13 …
问高一数学函数概念问题怎么感觉高一的函数概念好抽象啊,什么定义区,值域,都看书看不懂,特别是对于: 2020-05-17 …
建立角色服务有两个目的:为数据库应用管理特权和为()管理特权。 2020-05-31 …
实系数一元二次方程的系数概念ax^2+bx+c=0请问abc都要是实数嘛?特别是c,也一定要是实数 2020-06-06 …
要求判别键盘输入字符的类别.可以根据输入字符的ASCII码来判别类型由ASCII码表可知ASCII 2020-06-09 …
三颗骰子得出的点数概率问题甩出三颗骰子...得到的总和为3,4,5,.16,17,18请问出现各个 2020-06-17 …
阅读与思考婆罗摩笈多(Brahmagupta),是一位印度数学家和天文学家,书写了两部关于数学和天 2020-06-28 …
为什么说远处星球的光还没到达地球?难道宇宙这么大,就没有很多星球的光到了以后把夜空弄亮吗?如题,3 2020-07-22 …
英语翻译摘要:留数定理是复变函数中重要的工具与概念,需要正确理解孤立奇点的概念与孤立奇点的分类和函 2020-07-26 …
掷3次色子,朝上数字和为3的倍数,概率为多少 2020-11-25 …