早教吧作业答案频道 -->数学-->
在四面体P-ABC中,PA⊥平面ABC,△ABC为正三角形,PA=2,AB=3,则该四面体外接球的表面积等于.
题目详情
在四面体P-ABC中,PA⊥平面ABC,△ABC为正三角形,PA=2,AB=3,则该四面体外接球的表面积等于___.
▼优质解答
答案和解析
由题意画出几何体的图形如图,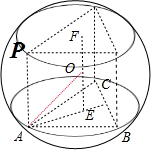
把A、B、C、P扩展为三棱柱,
上下底面中心连线的中点与A的距离为球的半径,
∵AB=3,△ABC为正三角形,
∴AE=
.
∵PA=2,∴AO=
=2.
所求球的表面积为:4π×22=16π.
故答案为:16π.

把A、B、C、P扩展为三棱柱,
上下底面中心连线的中点与A的距离为球的半径,
∵AB=3,△ABC为正三角形,
∴AE=
| 3 |
∵PA=2,∴AO=
| 3+1 |
所求球的表面积为:4π×22=16π.
故答案为:16π.
看了 在四面体P-ABC中,PA⊥...的网友还看了以下:
三角形的面积s=12(a+b+c)r,a,b,c为其边长,r为内切圆的半径,利用类比法可以得出四面 2020-05-02 …
下列命题是真命题的是()A.有两个面相互平行,其余各面都是平行四边形的多面体是棱柱B.正四面体是四 2020-05-13 …
请将下列概念进行分类,平行四边形,平行六面体,平面图形,菱形,正方形,三菱锥,三角形,等腰三角行, 2020-06-02 …
如何区分下列单体?1)斜方双锥,四方双锥和八面体2)斜方四面体,四方四面体,四面体 2020-07-05 …
阅读下面文段,在横线处填上恰当的喻体四面是柳枝篱笆,篱笆上爬满了豆角秧,豆角秧里还夹杂着喇叭花藤萝 2020-07-12 …
三角形的面积,a,b,c为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为 2020-07-23 …
设三角形ABC的三边长分别是a,b,c,三角形ABC的面积为S,内切圆的半径r=2S/a+b+c, 2020-07-31 …
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r=2Sa+b+c,类比 2020-07-31 …
若P是正四面体.若P是正四面体内一点,P到各面距离之和是一个定值,这个定值等于A正四面体的棱长B正 2020-07-31 …
(1)若三角形的内切圆半径为r,三边的长分别为a,b,c,则三角形的面积S=12r(a+b+c), 2020-08-01 …