已知两定点F1(-0)F2(0)满足条||-||=2的点P的轨迹是曲线C直线y=kx-2与曲线C交于A、B两点且|AB|=.(1)求曲线C的方程;(2)若曲线C上存在一点D使+=m求m的值及点D
(1)求曲线C的方程;
(2)若曲线C上存在一点D 使 ![]() +
+ ![]() =m
=m ![]() 求m的值及点D到直线AB的距离.
求m的值及点D到直线AB的距离.
解:(1)由双曲线的定义可知曲线C是以F 1 (- ![]() 0) F 2 (
0) F 2 ( ![]() 0)为焦点的双曲线的左半支
0)为焦点的双曲线的左半支
且c= ![]() 2a=2 a=1 故b=1 所以轨迹C的方程是x 2 -y 2 =1(x<0).
2a=2 a=1 故b=1 所以轨迹C的方程是x 2 -y 2 =1(x<0).
(2)设A(x 1 y 1 ) B(x 2 y 2 ) 由题意得方程组 
消去y 得(1-k 2 )x 2 +4kx-5=0.
又已知直线与曲线C交于A、B两点 故有 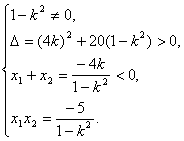
解得- ![]() <k<-1.
<k<-1.
∵|AB|= ![]() |x 2 -x 1 |
|x 2 -x 1 |
= ![]() ·
· ![]() =2
=2 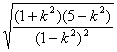 =
= ![]() ∴
∴ ![]() .
.
设t=k 2 得7t 2 -23t-20=0 (t-4)(7t+5)=0.
∴t=4 t= ![]() (舍去).
(舍去).
又由k 2 =4 舍去k=2 得k=-2 于是直线AB的方程为y=-2x-2
即2x+y+2=0.
由 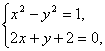 解得
解得 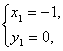
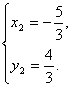 .
.
不妨设 ![]() =(-1,0),
=(-1,0), ![]() =(
=( ![]() ,
, ![]() ) 由
) 由 ![]() +
+ ![]() =m
=m ![]() 故有
故有 ![]() =(
=( ![]()
![]() ).
).
将D点坐标代入曲线C的方程 得 ![]() =1.解得m=±
=1.解得m=± ![]() 但当m=
但当m= ![]() 时 点D在双曲线右支上 不合题意 ∴m=
时 点D在双曲线右支上 不合题意 ∴m= ![]() .
.
点D的坐标为( ![]()
![]() ) D到AB的距离为
) D到AB的距离为 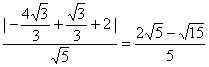 .
.
设A={X/X^2+4X=0},B={X/X^2+2(a+1)X+a^2-1=0,a属于R}.(1 2020-04-06 …
1.直线x+2y+1=0与抛物线(y^2)=4x的交点个数为?2.两平行直线2x-4y+5=0与x 2020-04-27 …
在梯形ABCD中,AB∥CD.(1)用尺规作图的方法,作∠的角平分线AF和梯形的高BG(保留作图痕 2020-05-01 …
如图23-48,在三角形ACD中,已知角ACD=120度,把三角形ACD绕顶点C逆时针旋转60度得 2020-05-16 …
1.已知P={y|y=x平方-2x+3,0大于等于x小于等于3},Q={x|y=根号下x-a}.( 2020-06-12 …
已知圆C:(x-3)+(y-4)=4,直线l1过定点A(1,0)(1)若l1与圆相切,求l1的方程 2020-06-27 …
已知圆C:(x-3)^2+(y-4)^2=4,直线L过定点A(1,0)1.若L与圆相切,求L的方程 2020-06-27 …
解析几何,高中已知圆C:(x-3)²+(y-4)²=4,直线L1过定点A(1,0)若L1与圆相交与 2020-08-02 …
若双曲线x^2/4-y^2/5=1与椭圆x^2/z^2+y^2/16=1有公共焦点,且z>0,则z= 2020-10-31 …
已知集合A={x|-3大于等于x小于等于2},B={x|x>m}.(1)若A交B不等于空集,求实数m 2020-11-12 …