早教吧作业答案频道 -->数学-->
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).(1)求直线BD和抛物线的解析式;(2)若BD与抛物线的对称轴交于点M,点N
题目详情
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
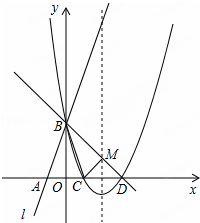
(1)求直线BD和抛物线的解析式;
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标;
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由;
(4)点Q是抛物线对称轴上一动点,是否存在点Q使得|BQ-CQ|的值最大,若存在,请直接写出点Q的坐标;若不存在,请说明理由.

(1)求直线BD和抛物线的解析式;
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标;
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由;
(4)点Q是抛物线对称轴上一动点,是否存在点Q使得|BQ-CQ|的值最大,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
 (1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
(1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
∴A(-1,0),B(0,3);
∵把△AOB沿y轴翻折,点A落到点C,
∴C(1,0).
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,
∴
,
解得k=-1,b=3,
∴直线BD的解析式为:y=-x+3.
设抛物线的解析式为:y=a(x-1)(x-3),
∵点B(0,3)在抛物线上,
∴3=a×(-1)×(-3),
解得:a=1,
∴抛物线的解析式为:y=(x-1)(x-3)=x2-4x+3.
(2)抛物线的解析式为:y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,-1).
直线BD:y=-x+3与抛物线的对称轴交于点M,令x=2,得y=1,
∴M(2,1).
设对称轴与x轴交点为点F,则CF=FD=MF=1,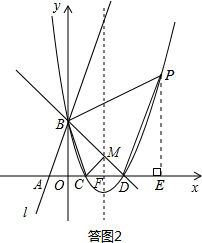
∴△MCD为等腰直角三角形.
∵以点N、B、D为顶点的三角形与△MCD相似,
∴△BND为等腰直角三角形.
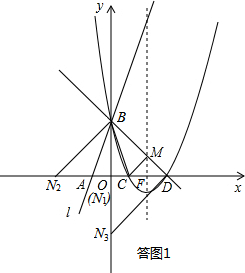
如答图1所示:
(I)若BD为斜边,则易知此时直角顶点为原点O,
∴N1(0,0);
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,
∴N2(-3,0);
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,
∴N3(0,-3).
∴满足条件的点N坐标为:(0,0),(-3,0)或(0,-3).
(3)假设存在点P,使S△PBD=6,设点P坐标为(m,n).
(I)当点P位于直线BD上方时,如答图2所示:
过点P作PE⊥x轴于点E,则PE=n,DE=m-3.
S△PBD=S梯形PEOB-S△BOD-S△PDE=
(3+n)•m-
×3×3-
(m-3)•n=6,
化简得:m+n=7 ①,
∵P(m,n)在抛物线上,
∴n=m2-4m+3,
代入①式整理得:m2-3m-4=0,
解得:m1=4,m2=-1,
∴n1=3,n2=8,
 ∴P1(4,3),P2(-1,8);
∴P1(4,3),P2(-1,8);
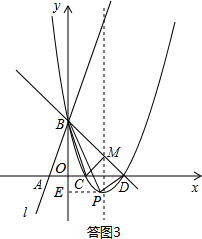
(II)当点P位于直线BD下方时,如答图3所示:
过点P作PE⊥y轴于点E,则PE=m,OE=-n,BE=3-n.
S△PBD=S梯形PEOD+S△BOD-S△PBE=
(3+m)•(-n)+
×3×3-
(3-n)•m=6,
化简得:m+n=-1 ②,
∵P(m,n)在抛物线上,
∴n=m2-4m+3,
代入②式整理得:m2-3m+4=0,△=-7<0,此方程无解.
故此时点P不存在.
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(-1,8).
(4)∵B(0,3),C(1,0),
∴直线BC的解析式为:y=-3x+3,
∴当x=2时,y=-3×2+3=-3.
∴点Q(2,-3).
 (1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
(1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,∴A(-1,0),B(0,3);
∵把△AOB沿y轴翻折,点A落到点C,
∴C(1,0).
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,
∴
|
解得k=-1,b=3,
∴直线BD的解析式为:y=-x+3.
设抛物线的解析式为:y=a(x-1)(x-3),
∵点B(0,3)在抛物线上,
∴3=a×(-1)×(-3),
解得:a=1,
∴抛物线的解析式为:y=(x-1)(x-3)=x2-4x+3.
(2)抛物线的解析式为:y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,-1).
直线BD:y=-x+3与抛物线的对称轴交于点M,令x=2,得y=1,
∴M(2,1).
设对称轴与x轴交点为点F,则CF=FD=MF=1,

∴△MCD为等腰直角三角形.
∵以点N、B、D为顶点的三角形与△MCD相似,
∴△BND为等腰直角三角形.
如答图1所示:
(I)若BD为斜边,则易知此时直角顶点为原点O,
∴N1(0,0);
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,
∴N2(-3,0);
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,
∴N3(0,-3).
∴满足条件的点N坐标为:(0,0),(-3,0)或(0,-3).
(3)假设存在点P,使S△PBD=6,设点P坐标为(m,n).
(I)当点P位于直线BD上方时,如答图2所示:
过点P作PE⊥x轴于点E,则PE=n,DE=m-3.
S△PBD=S梯形PEOB-S△BOD-S△PDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
化简得:m+n=7 ①,
∵P(m,n)在抛物线上,
∴n=m2-4m+3,
代入①式整理得:m2-3m-4=0,
解得:m1=4,m2=-1,
∴n1=3,n2=8,
 ∴P1(4,3),P2(-1,8);
∴P1(4,3),P2(-1,8);(II)当点P位于直线BD下方时,如答图3所示:
过点P作PE⊥y轴于点E,则PE=m,OE=-n,BE=3-n.
S△PBD=S梯形PEOD+S△BOD-S△PBE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
化简得:m+n=-1 ②,
∵P(m,n)在抛物线上,
∴n=m2-4m+3,
代入②式整理得:m2-3m+4=0,△=-7<0,此方程无解.
故此时点P不存在.
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(-1,8).
(4)∵B(0,3),C(1,0),
∴直线BC的解析式为:y=-3x+3,
∴当x=2时,y=-3×2+3=-3.
∴点Q(2,-3).
看了如图所示,直线l:y=3x+3...的网友还看了以下:
如图,把含有45°角的三角板顶点C放在y轴上,三角板斜边AB放在x轴上,AB=4,抛物线l经过三角 2020-04-26 …
已经知道抛物线的标准解析式为Y=2PX^2,或Y=-2PX^2,A点(a,b)在抛物线上.求过此点 2020-06-05 …
牧场物语放牧请问在牧场物语中,放牧的时间怎么计算?比如我第一天7点开始放牧,9点睡觉,把动物放在外 2020-06-20 …
为什么不能把自己抱起来?为什么呢?有人说没有支撑点,那你把自己手抬起来的支撑点在哪呢?还有说施力物 2020-06-22 …
(2013•恩施州)如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴 2020-06-23 …
朱熹的“理生万物”观点属于[]A.“理”和物质结合起来的辩证法思想B.“理”是世界本原的朴素唯物主 2020-07-28 …
(2014•东营)如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落 2020-11-13 …
南非世界杯期间,章鱼保罗预测了8场比赛,准确率100%,他们都把章鱼保罗视为圣物。把章鱼保罗视为圣物 2021-01-07 …
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛 2021-01-11 …
已知数轴上某一点x.(1)把点x向右动一个单位,得到的数是x+1,若把点x向左移动一个已知数轴上某一 2021-02-05 …