早教吧作业答案频道 -->数学-->
已知平行四边形ABCD中,点E是BC的中点,在直线BA上截取BF=2AF,EF交BD于点G,则GDGB的值为.
题目详情
已知平行四边形ABCD中,点E是BC的中点,在直线BA上截取BF=2AF,EF交BD于点G,则
的值为___.
| GD |
| GB |
▼优质解答
答案和解析
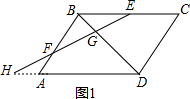 (1)如图1,点F在线段AB上时,设EF与DA的延长线交于H,
(1)如图1,点F在线段AB上时,设EF与DA的延长线交于H,
∵BC∥AD,
∴△EBF∽△HAF,
∴HA:BE=AF:BF=1:2,
即HA=
BE
∵BC∥AD,
∴△DHG∽△BEG,
∴BG:DG=BE:DH
∵BC=AD=2BE,
∴DH=AD+AH=2BE+
BE=
BE,
∴
=
;
(2)如图2,点F在线段BA的延长线上时,设EF与DA交于H,
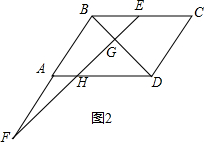 ∵BC∥AD,
∵BC∥AD,
∴△EBF∽△HAF,
∴HA:BE=AF:BF=1:2,
即HA=
BE,
∵BC∥AD,
∴△DHG∽△BEG,
∴BG:DG=BE:DH
∵BC=AD=2BE,
∴DH=AD+AH=2BE-
BE=
BE,
∴
=
.
故答案为:
或
.
 (1)如图1,点F在线段AB上时,设EF与DA的延长线交于H,
(1)如图1,点F在线段AB上时,设EF与DA的延长线交于H,∵BC∥AD,
∴△EBF∽△HAF,
∴HA:BE=AF:BF=1:2,
即HA=
| 1 |
| 2 |
∵BC∥AD,
∴△DHG∽△BEG,
∴BG:DG=BE:DH
∵BC=AD=2BE,
∴DH=AD+AH=2BE+
| 1 |
| 2 |
| 5 |
| 2 |
∴
| GD |
| GB |
| 5 |
| 2 |
(2)如图2,点F在线段BA的延长线上时,设EF与DA交于H,
 ∵BC∥AD,
∵BC∥AD,∴△EBF∽△HAF,
∴HA:BE=AF:BF=1:2,
即HA=
| 1 |
| 2 |
∵BC∥AD,
∴△DHG∽△BEG,
∴BG:DG=BE:DH
∵BC=AD=2BE,
∴DH=AD+AH=2BE-
| 1 |
| 2 |
| 3 |
| 2 |
∴
| GD |
| GB |
| 3 |
| 2 |
故答案为:
| 5 |
| 2 |
| 3 |
| 2 |
看了已知平行四边形ABCD中,点E...的网友还看了以下:
在三角形ABC中,内角A,B,C所对的边分别是a,b,c,若此三角形面积S=a平方-(b-c)平方 2020-05-16 …
当游客登上海岛时,该岛表面形状为三角形,三边A,B,C满足以下关系,3(A平方+B平方+C平方)= 2020-05-16 …
在三角形ABC中,角A、B、C的对边为a,b,c,面积S=a的平方-(b-c)的平方,则sinA= 2020-05-16 …
..速速回答1.(3a-4)的平方=252.2的24次方可以被再60和70之间的两个数整除,这两个 2020-06-04 …
设a.b.c分别是三角形三边的长,化简:根号(a-b+c)的平方+根号(b-c-a)的平方.平方都 2020-06-06 …
二次根试已知a,b,c是△ABC的三边化简:根号下“(a-b-c)的平方”-“根号下(b-a+c) 2020-06-17 …
诺三角行ABC的三边a,b,c满足(a+b+c)的平方,试说明三角行ABC为等边三角行.打错了~满 2020-06-29 …
1.若平行四边形ABCD相似于平行四边形A'B'C'D',平行四边形ABCE的面积:平行四边形A' 2020-08-01 …
人教版必修5课本的一道数学题三角形ABC三边分别为a,b,c,边BC,CA,AB上的中线分别记为m 2020-08-02 …
已知三角形ABC的三边长为a、b、c,有b+c=8,面积S=a的平方-[(b-c)的平方],求Sma 2021-02-07 …