根据经典理论,金属导体中电流的微观表达式为I=nvSe,其中n为金属导体中每单位体积内的自由电子数,v为导体中自由电子沿导体定向移动的速率,S为导体的横截面积,e为自由电子
根据经典理论,金属导体中电流的微观表达式为I=nvSe,其中n为金属导体中每单位体积内的自由电子数,v为导体中自由电子沿导体定向移动的速率,S为导体的横截面积,e为自由电子的电荷量.如图11所示,两段长度和材料完全相同、各自粗细均匀的金属导线ab、bc,圆横截面的半径之比为r ab ∶r bc =1∶4,串联后加上电压U,则 ( )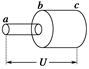
| A.两导线内的自由电子定向移动的速率之比为v ab ∶v bc =1∶4 |
| B.两导线内的自由电子定向移动的速率之比为v ab ∶v bc =4∶1 |
| C.两导线的电功率之比为P ab ∶P bc =4∶1 |
| D.两导线的电功率之比为P ab ∶P bc =16∶1 |
D
解析
生物体在减数分裂时非等位基因是怎么自由组合的?在生物体通过减数分裂形成配子时,随着非同源染色体的自 2020-05-17 …
下图为人体体细胞中的一对基因位于一对染色体上的示意图。下列关于图解的叙述不正确的是[]A.染色体上 2020-06-17 …
如图为普通小麦(异源六倍体)自然起源过程示意图.据材料分析有关问题:(1)普通小麦自然起源过程中, 2020-06-26 …
走进新学校一个多月来,班级对每个同学做评价。王芳自己认为在班级集体建设中经常参加出黑板报,积极参加 2020-07-10 …
物理题怎么判断中心天体是否自转,怎么判断中心天体不自传,做题的时候,比如,给出重力加速度,就知道.. 2020-11-24 …
I.某一反应体系中有反应物和生成物共五种物质:O2、H2CrO4、Cr(OH)3、H2O、H2O2。 2020-12-25 …
(18分)I.某一反应体系中有反应物和生成物共五种物质:O2、H2CrO4、Cr(OH)3、H2O、 2020-12-25 …
下列关于自由落体加速度的说法中正确的是()A.任何物体下落的加速度都是10m/s2B.在同一个地区所 2021-01-22 …
关于自由落体运动,下列说法正确的是()A.任何物体在同一地方做自由落体运动的加速度是相同的B.物体做 2021-01-22 …
关于自由落体运动,下列说法不正确的是()A.所有物体的自由落体运动的规律都是相同的B.只在重力作用下 2021-01-22 …