早教吧作业答案频道 -->数学-->
如图,将一副三角板按如图所示方式摆放,点A,B,D在同一条直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,DE=8,试求BD的长.
题目详情
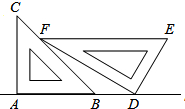 如图,将一副三角板按如图所示方式摆放,点A,B,D在同一条直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,DE=8,试求BD的长.
如图,将一副三角板按如图所示方式摆放,点A,B,D在同一条直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,DE=8,试求BD的长.▼优质解答
答案和解析
考点:
勾股定理 含30度角的直角三角形 等腰直角三角形
专题:
分析:
过E作EG⊥l于G,过F作FH⊥l于H,求出∠GED的度数,利用三角函数的知识即可求出EG的长度,在△FBH和△FHD中,分别求出HB,HD的长度,然后用HD-HB的长度即可求得BD的长.
过E作EG⊥l于G,过F作FH⊥l于H,∵∠EFD=30°,∠EDF=90°∴∠FED=60°,∴∠GED=30°,∴GE=32DE=43cm,∵EF∥AD,∴FH=EG=43.∵∠C=45°,∴BH=FH=43,∵∠FDH=∠EFD=30°,∴DH=3FH=12,∴BD=(12-43)cm.
点评:
本题考查了勾股定理和三角函数的知识,解答本题的关键是根据三角函数的知识在直角三角形中求出直角边的长度,难度适中.
考点:
勾股定理 含30度角的直角三角形 等腰直角三角形
专题:
分析:
过E作EG⊥l于G,过F作FH⊥l于H,求出∠GED的度数,利用三角函数的知识即可求出EG的长度,在△FBH和△FHD中,分别求出HB,HD的长度,然后用HD-HB的长度即可求得BD的长.
过E作EG⊥l于G,过F作FH⊥l于H,∵∠EFD=30°,∠EDF=90°∴∠FED=60°,∴∠GED=30°,∴GE=32DE=43cm,∵EF∥AD,∴FH=EG=43.∵∠C=45°,∴BH=FH=43,∵∠FDH=∠EFD=30°,∴DH=3FH=12,∴BD=(12-43)cm.
点评:
本题考查了勾股定理和三角函数的知识,解答本题的关键是根据三角函数的知识在直角三角形中求出直角边的长度,难度适中.
看了如图,将一副三角板按如图所示方...的网友还看了以下:
如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,试说明E,F关于AD对称 2020-05-13 …
如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2 2020-05-16 …
在正方形ABCD-A1B1C1D1中,E,F,G,H,M,N分别是正方形的棱A1A,AB,BC,C 2020-05-16 …
把等边三角形ABC和等边三角形BCD拼合在一起,E在AB上移动,F在BD上移动,且AE=BF,试说 2020-05-21 …
如图,在三角形ABC中,点D.E在边BC上,角CAE=角B,E是CD的中点,且AD平分角BAE.1 2020-06-08 …
直角梯形ABCD,AD‖BC,∠BCD=90°,AB=10,BC=16,E在BC上,F在AC上,且 2020-07-21 …
如图,在△ABC中,BE是∠ABC的内角平分线,CE是∠ACB的外角平分线,BE、CE交于E点,试 2020-07-27 …
本人完全不会.1,设方阵A满足A3=0,试证明E-A可逆,且(E-A)-1=E+A+A2.2,.设 2020-07-31 …
已知:如图,△ABC中,AD⊥BC于D,E是CA延长线上一点,EG⊥BC于G,交AB于F,AD是∠ 2020-08-01 …
设A为主对角线元素均为零的四阶实对称可逆矩阵,E为四阶单位矩阵B=0000000000k0000l 2020-08-02 …