早教吧作业答案频道 -->物理-->
如图所示,在xoy平面的第一象限内,分布有沿x轴负方向的场强E=43×104N/C的匀强电场,第四象限内分布有垂直纸面向里的磁感应强度B1的匀强磁场,第二、三象限内分布有垂直纸面向里的磁感
题目详情
如图所示,在xoy平面的第一象限内,分布有沿x轴负方向的场强E=
×104N/C的匀强电场,第四象限内分布有垂直纸面向里的磁感应强度B1的匀强磁场,第二、三象限内分布有垂直纸面向里的磁感应强度B2的匀强磁场.在x轴上开有一个小孔P,距坐标原点3cm,P处连接有一段长度d=1cm内径不计,可来回抽动的准直管,管内由于静电屏蔽没有电场.粒子源S自管底部发射a粒子,假设发射的a粒速度大小v均为2×105m/s.已知a粒子带正电,比荷为
=5×107C/kg,重力不计,求:
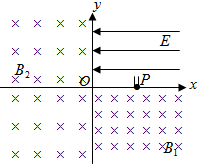
(1)经过准直管进入电场中运动的a粒子,第一次到达y轴的位置与O点的距离范围;
(2)要使第一次到达y轴离O点最远的粒子和最近的粒子能在y负半轴离O点1cm处相遇,求磁感应强度B1和B2各为多大?
| 4 |
| 3 |
| q |
| m |
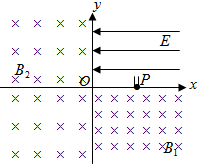
(1)经过准直管进入电场中运动的a粒子,第一次到达y轴的位置与O点的距离范围;
(2)要使第一次到达y轴离O点最远的粒子和最近的粒子能在y负半轴离O点1cm处相遇,求磁感应强度B1和B2各为多大?
▼优质解答
答案和解析
(1)粒子在第一象限中做类平抛运动
竖直方向:y=vt;
水平方向:x=
at2;
加速度为:a=
=
×1012m/s2,
解得:t=3×10-7s;y=6cm,
因准直管来回抽动,故打在y轴上的范围为[6cm,7cm].
(2)设粒子在y轴射出电场的速度方向与y轴正方向夹角为θ,
则有:tanθ=
=1,θ=450;v′=
v,
若粒子离开电场经B2磁场偏转,最远的粒子轨迹如图虚线所示,
最近的粒子轨迹如图实线所示,经过第四象限偏转后再与最远的粒子相交于y轴.
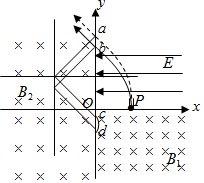
在B1磁场中圆周运动半径:
R1=
=
×10-2cm,
由qv′B1=
得,磁感应强度:
B1=
=0.8T.
在B2磁场中圆周运动半径:
R2=
=4
×10-2cm,
由qv′B2=
得,磁感应强度:
B2=
=0.1T.
答:(1)经过准直管进入电场中运动的a粒子,第一次到达y轴的位置与O点的距离范围为[6cm,7cm];
竖直方向:y=vt;
水平方向:x=
| 1 |
| 2 |
加速度为:a=
| Eq |
| m |
| 2 |
| 3 |
解得:t=3×10-7s;y=6cm,
因准直管来回抽动,故打在y轴上的范围为[6cm,7cm].
(2)设粒子在y轴射出电场的速度方向与y轴正方向夹角为θ,
则有:tanθ=
| at |
| v |
| 2 |
若粒子离开电场经B2磁场偏转,最远的粒子轨迹如图虚线所示,
最近的粒子轨迹如图实线所示,经过第四象限偏转后再与最远的粒子相交于y轴.

在B1磁场中圆周运动半径:
R1=
| ||
|
| ||
| 2 |
由qv′B1=
| v′2 |
| R1 |
B1=
| v′2 |
| qR1 |
在B2磁场中圆周运动半径:
R2=
| ||
|
| 2 |
由qv′B2=
| v′2 |
| R2 |
B2=
| v′2 |
| qR2 |
答:(1)经过准直管进入电场中运动的a粒子,第一次到达y轴的位置与O点的距离范围为[6cm,7cm];
作业帮用户
2016-12-18
举报

看了 如图所示,在xoy平面的第一...的网友还看了以下:
为什么数列极限四则运算法则只能用于项数有限数列跟据数列极限四则运算加法法则,多个有极限数列之和的极 2020-06-27 …
1/2+1/3+1/5+1/8+1/13+1/21+...的极限是多少?不要瞎写~不可能没有极限吧 2020-06-27 …
请麻烦把数列的极限的概念说一下,还有回答几个问题数列3,3,3,3,3,……(一万个)的极限是3吗 2020-07-09 …
利用单调有界必有极限证明一下数列limxn存在,并求出极限1)x1=根号2……xn=根号(2x(n 2020-07-09 …
数列极限判断对错的题1、数列极限定义中的ε是个任意小的正数2、数列极限中的n有无穷多个,但只要找到 2020-07-15 …
一道数学找规律的题图一有1个三角形,图二有5个三角形,图三有9个三角形,第n个图形中有多少个三角形 2020-07-20 …
限制酶Ⅰ的识别序列和切点是-G↓CATCC-,限制酶Ⅱ的识别序列和切点是-↓GATC-。在质粒上有 2020-07-31 …
有极限一定有界吗1/X有极限,但是没界.但是不是说有极限一定有界,有界不一定有极限? 2020-07-31 …
单调有界数列一定有极限吗?lim=(1+1/x)exp(x)=e,这个极限是求证x->无穷时的极限 2020-08-02 …
极限问题若干超急不懂啊,1.一个式子是存在极限的另一个不存在极限,那么着两个式子相加可不可以说它们的 2020-11-07 …