早教吧作业答案频道 -->数学-->
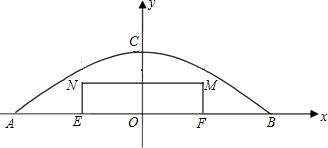
某公园有一个抛物线形状的观景拱桥ACB,其横截面如图所示,量得该拱桥占地面最宽处AB=20米,最高处点C距地面5米(即OC=5米)(1)分别以AB、OC所在直线为x轴、y轴,建立如图所示的平面直
题目详情
某公园有一个抛物线形状的观景拱桥ACB,其横截面如图所示,量得该拱桥占地面最宽处AB=20米,最高处点C距地面5米(即OC=5米)
(1)分别以AB、OC所在直线为x轴、y轴,建立如图所示的平面直角坐标系,求该抛物线的解析式;
(2)夜晚,公园沿着抛物线ACB用彩灯勾勒拱桥的形状;现公园管理处打算在观景拱桥ABC的横截面前放置一个长为10米的矩形广告牌EFMN,为安全起见,要求广告牌高拱桥的桥面至少0.35米,求矩形广告牌的最大高度,并说明理由.
(1)分别以AB、OC所在直线为x轴、y轴,建立如图所示的平面直角坐标系,求该抛物线的解析式;
(2)夜晚,公园沿着抛物线ACB用彩灯勾勒拱桥的形状;现公园管理处打算在观景拱桥ABC的横截面前放置一个长为10米的矩形广告牌EFMN,为安全起见,要求广告牌高拱桥的桥面至少0.35米,求矩形广告牌的最大高度,并说明理由.

▼优质解答
答案和解析
(1)根据题意,设抛物线解析式为y=ax2+c,
将点C(0,5),点B(10,0)代入,得:
,
解得:
.
故抛物线解析式为:y=-
x2+5;
(2)当x=5时,y=-
×25+5=3.75(m),
3.75-0.35=3.4(m).
答:矩形广告牌的最大高度为3.4m.
将点C(0,5),点B(10,0)代入,得:
|
解得:
|
故抛物线解析式为:y=-
| 1 |
| 20 |
(2)当x=5时,y=-
| 1 |
| 20 |
3.75-0.35=3.4(m).
答:矩形广告牌的最大高度为3.4m.
看了某公园有一个抛物线形状的观景拱...的网友还看了以下:
22222=2在个数之间填上适当的"+、-、×、÷"符号,是算式成立. 2020-04-09 …
1又2分之1与3分之2的和等于一个数3分之2,在个数是多少?(用方程解) 2020-05-16 …
我问一个问题,说:2.5与2.8哪个大,可不可以这样理解,把2看做整数,小数点后面的5是小数,2在 2020-05-20 …
(1/2)一个长方体木块,它的所有棱长之和为108厘米,它的长、宽、高之比是4:3:2,现在要将这 2020-06-03 …
笔算145×32时,先算得,因为这里的2在个位上,表示2个一,所以从位写起;再算得,因为这里的3在 2020-07-18 …
1,某城市有学校500所,其中大学10所,中学200所,小学290所,现在取50所学校作为一个样本 2020-07-19 …
立体几何的2个小疑问..求二面角A1—AB—B1和求面A1AB与面ABB1所成的角一样吗?2.在求 2020-07-31 …
问题引入:在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值.必然|-2|就表示-2这个点到 2020-08-03 …
1:放松消遣和娱乐.2在个人的业余时间.3对电影4电视感兴趣5个人发展6大众传媒7成为一个热点话题8 2020-12-16 …
如下图所示,一个物体M=250g放在右边的托盘上,导致两个托盘同时加速2.45ms^-2.两个托盘自 2021-01-23 …