早教吧作业答案频道 -->数学-->
如图,正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当点M在BC上运动时,保持AM和MN垂直.(1)证明:Rt△ABM∽Rt△MCN;(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M
题目详情
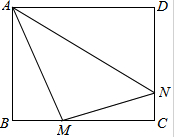
如图,正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当点M在BC上运动时,保持AM和MN垂直.
(1)证明:Rt△ABM∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN面积最大,并求出最大面积;
(3)当点M运动到什么位置时,Rt△ABM∽Rt△AMN?

(1)证明:Rt△ABM∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN面积最大,并求出最大面积;
(3)当点M运动到什么位置时,Rt△ABM∽Rt△AMN?
▼优质解答
答案和解析
(1)证明:在正方形ABCD中,∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠BAM+∠AMB=90°,
∴∠BAM=∠CMN,
∴Rt△ABM∽Rt△MCN;
(2) ∵Rt△ABM∽Rt△MCN,BM=x,
∴AB:MC=BM:CN,即
=
,
整理得:CN=
,
∴y=S梯形ABCN=
×(
+4)×4=-
x2+2x+8=-
(x-2)2+10(0<x<4),
则当x=2,即M点运动到BC的中点时,梯形ABCN的面积最大,最大值为10;
(3)当点M运动到BC中点时,Rt△ABM∽Rt△AMN,理由如下:
∵∠B=∠AMN=90°,
∴要使Rt△ABM∽Rt△AMN,必须有
=
,即BM=
,
由(1)知
=
,即MC=
,
∴BM=MC,
则当点M运动到BC的中点时,Rt△ABM∽Rt△AMN.
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠BAM+∠AMB=90°,
∴∠BAM=∠CMN,
∴Rt△ABM∽Rt△MCN;
(2) ∵Rt△ABM∽Rt△MCN,BM=x,
∴AB:MC=BM:CN,即
| 4 |
| 4-x |
| x |
| CN |
整理得:CN=
| -x2+4x |
| 4 |
∴y=S梯形ABCN=
| 1 |
| 2 |
| -x2+4x |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
则当x=2,即M点运动到BC的中点时,梯形ABCN的面积最大,最大值为10;
(3)当点M运动到BC中点时,Rt△ABM∽Rt△AMN,理由如下:
∵∠B=∠AMN=90°,
∴要使Rt△ABM∽Rt△AMN,必须有
| AB |
| AM |
| BM |
| MN |
| AB•MN |
| AM |
由(1)知
| AM |
| MN |
| AB |
| MC |
| AB•MN |
| AM |
∴BM=MC,
则当点M运动到BC的中点时,Rt△ABM∽Rt△AMN.
看了如图,正方形ABCD的边长为4...的网友还看了以下:
问几个c问题1,设x=2.5,y=4.7,a=7,则x+a%3*(int)(x+y)%2/4=2, 2020-04-08 …
如图,C为圆O直径AB上的一动点,过点C的直线交圆O于D、E两点,且∠ACD=45°,DF⊥AB于 2020-04-25 …
大队委为学校设计一个小运动场.运动场设置5条跑道,每条跑道宽1.2m,最内侧半圆跑道的直径60m, 2020-06-04 …
如图,在直角坐标系中,正方形ABOD的边长为a,O为原点,点B在x轴的负半轴上,点D在y轴的正半轴 2020-06-14 …
在红蜡块的演示实验中,假设蜡块在从静止匀加速上升的同时,将玻璃管沿水平方向向右匀加速移动.那么蜡块 2020-07-06 …
小球左右来回摆动,若其运动到右边最高处的那一刻绳子断了,假设摆球所受的力同时都消失.则摆球()A. 2020-07-10 …
一物体在介质中按规律x=ct^3作直线运动,c为一常量.设介质对物体的阻力正比于速度的平方.求物体 2020-07-11 …
解析几何已知圆C:x^2+y^2=4.(1)直线l过点p(1,2),且与圆c交于A、B两点,若|A 2020-08-02 …
论语上说:土不可不弘毅,任重而道远。这说明()A.设立的目标要可行B.自强的人,总会把目标转化为行动 2020-11-03 …
直线与圆的方程,难度适中的题目已知圆C方程为x^2+y^2=4(1)直线L过点P(1,2)且与圆C交 2020-12-03 …