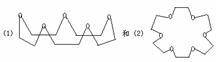
C.J.Pedersen教授由于发明了冠醚而获得诺贝尔奖。大多数醚因形似“王冠”故称冠醚。如下列关于冠醚的说法正确的是(
C.J.Pedersen 教授由于发明了冠醚而获得诺贝尔奖。大多数醚因形似 “ 王冠 ” 故称冠醚。如
| |
下列关于冠醚的说法正确的是 ( )
A . 冠醚属于烃类 B . (2) 式与葡萄糖互为同分异构体
C . 冠醚能燃烧生成 CO 2 和 H 2 O D . (1) 式和 (2) 式互为同系物
C
已知四分之派小于阿尔法小于四分之三派,零小于贝塔小于四分之派,cos(四分之派+阿尔法)等于负五分 2020-04-27 …
有关贝加尔湖的说法正确的有( )。A、世界上最古老的湖B、世界上:最深的湖C、世界上蓄水量最大的淡 2020-05-20 …
二角和与差的三角函数阿尔法,贝他属于(0,90°),tan阿尔法=4/3,tan贝他=1/7,阿尔 2020-06-15 …
若sin阿尔法+sin贝达=1/根号3(cos贝答-cos阿尔法),阿尔法,贝答∈(0,派),则阿 2020-06-15 …
为什么三角形的一个边长等于一个边乘以正弦比就知道其中2个角一个阿尔法一个贝塔和这2角的夹边a为什么 2020-07-18 …
阅读材料,回答问题。(14分)材料一:北非某区域图材料二:阿尔及尔与贝沙尔气候统计资料(1)描述该 2020-07-22 …
如图,∠埃尔法+∠贝塔是三角形ABC外交(1)∠埃尔法+∠贝塔能等于180°吗?为什么(2)设∠埃 2020-07-24 …
请懂物理的朋友回答下:关于盖革计数器本身辐射的问题前天入手了一台苏军的DP-5(ДП-5)盖革计数器 2020-11-17 …
关于诺贝尔物理学奖,请你判断哪个是不正确的诺贝尔物理学奖只发给个人,并且每年的获奖人数不超过3人.诺 2020-11-17 …
下列关于科学技术的描述正确的是()A.前苏联的切尔诺贝利核电站的泄漏事故和日本福岛第一核电站爆炸说明 2020-11-24 …