已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc<0；②b<a+c；③4a+2b+c>0；④2c<3b；⑤a+b<m（am+b）（m≠1的实数），其中结论正确的个数有（）A.2个B.

Question

已知二次函数y=ax²+bx+c （a≠0）的图象如图所示，有下列5个结论：
①abc<0；　②b<a+c；　③4a+2b+c>0；④2c<3b；⑤a+b<m （am+b）（m≠1的实数），其中结论正确的个数有（　　）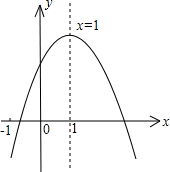

A. 2个

B. 3个

C. 4个

D. 5个

Answer 1

①图象开口向下，与y轴交于正半轴，对称轴为x=1，能得到：a<0，c>0，-(b)/(2a)=1，
∴b=-2a>0，
∴abc<0，此结论正确；

②当x=-1时，由图象知y<0，
把x=-1代入解析式得：a-b+c<0，
∴b>a+c，
∴②错误；

③图象开口向下，与y轴交于正半轴，对称轴为x=1，
能得到：a<0，c>0，-(b)/(2a)=1，
所以b=-2a，
所以4a+2b+c=4a-4a+c>0．
∴③正确；

④∵由①②知b=-2a且b>a+c，
∴2c<3b，④正确；

⑤∵x=1时，y=a+b+c（最大值），
x=m时，y=am²+bm+c，
∵m≠1的实数，
∴a+b+c>am²+bm+c，
∴a+b>m（am+b）．
∴⑤错误．
故选：B．