早教吧作业答案频道 -->数学-->
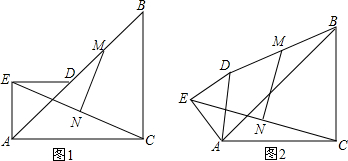
如图,△ACB、△AED都为等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连CE,M、N分别为BD、CE的中点.(1)求证:MN=12CE;(2)如图,将△ADE绕点A逆时针旋转一个锐角后,(1)中结论是否仍成
题目详情
如图,△ACB、△AED都为等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连CE,M、N分别为BD、CE的中点.
(1)求证:MN=
CE;
(2)如图,将△ADE绕点A逆时针旋转一个锐角后,(1)中结论是否仍成立?若成立,请证明;
(3)求证:MN⊥CE.
(1)求证:MN=
| 1 |
| 2 |
(2)如图,将△ADE绕点A逆时针旋转一个锐角后,(1)中结论是否仍成立?若成立,请证明;
(3)求证:MN⊥CE.

▼优质解答
答案和解析
(1)证明:延长DN交AC于F,连BF,
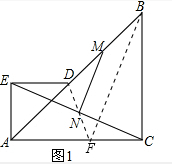
∵△ACB和△AED是等腰直角三角形,∠AED=∠ACB=90°,DE=AE,AC=BC,
∴∠EAD=∠EDA=∠BAC=45°,
∴DE∥AC,
∴∠DEN=∠FCN,
在△DEN和△FCN中,
,
∴△DEN≌△FCN(ASA),
∴DE=FC,DN=NF,
∴AE=FC,
∵M是BD中点,
∴MN是△BDF的中位线,
∴MN=
BF,
∵∠EAD=∠BAC=45°,
∴∠EAC=∠ACB=90°,
在△CAE和△BCF中,
,
∴△CAE≌△BCF(SAS),
∴BF=CE,
∴MN=
CE;
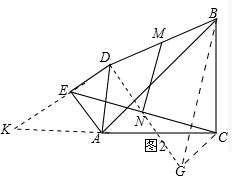
(2)证明:延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,
∵M为BD中点,
∴MN是△BDG的中位线,
∴BG=2MN,
在△EDN和△CGN中,
,
∴△EDN≌△CGN(SAS),
∴DE=CG=AE,∠GCN=∠DEN,
∴DE∥CG,
∴∠KCG=∠CKE,
∵∠CAE=45°+∠DAB+45°=90°+∠DAB,
∴∠EAK=90°-∠DAB,
∴∠CKE=∠KCG=∠DAB,
∴∠BCG=90°+∠DAB,
在△CAE和△BCG中,
,
∴△CAE≌△BCG(SAS),
∴BG=CE,
∵BG=2MN,
∴CE=2MN.
(3)∵△CAE≌△BCG,
∴∠ACE=∠CBG,
∵∠ACE+∠BCE=90°,
∴∠CBG+∠BCE=90°,
即BG⊥CE,
∵MN∥BG,
∴MN⊥CE.

∵△ACB和△AED是等腰直角三角形,∠AED=∠ACB=90°,DE=AE,AC=BC,
∴∠EAD=∠EDA=∠BAC=45°,
∴DE∥AC,
∴∠DEN=∠FCN,
在△DEN和△FCN中,
|
∴△DEN≌△FCN(ASA),
∴DE=FC,DN=NF,
∴AE=FC,
∵M是BD中点,
∴MN是△BDF的中位线,
∴MN=
| 1 |
| 2 |
∵∠EAD=∠BAC=45°,
∴∠EAC=∠ACB=90°,
在△CAE和△BCF中,
|
∴△CAE≌△BCF(SAS),
∴BF=CE,
∴MN=
| 1 |
| 2 |
(2)证明:延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,

∵M为BD中点,
∴MN是△BDG的中位线,
∴BG=2MN,
在△EDN和△CGN中,
|
∴△EDN≌△CGN(SAS),
∴DE=CG=AE,∠GCN=∠DEN,
∴DE∥CG,
∴∠KCG=∠CKE,
∵∠CAE=45°+∠DAB+45°=90°+∠DAB,
∴∠EAK=90°-∠DAB,
∴∠CKE=∠KCG=∠DAB,
∴∠BCG=90°+∠DAB,
在△CAE和△BCG中,
|
∴△CAE≌△BCG(SAS),
∴BG=CE,
∵BG=2MN,
∴CE=2MN.
(3)∵△CAE≌△BCG,
∴∠ACE=∠CBG,
∵∠ACE+∠BCE=90°,
∴∠CBG+∠BCE=90°,
即BG⊥CE,
∵MN∥BG,
∴MN⊥CE.
看了如图,△ACB、△AED都为等...的网友还看了以下:
超难初中几何题已知:圆O,PA,PB分别切圆O于AB两点,在劣弧AB上任意一点C,过C做圆O的切线交 2020-03-30 …
读图,位于东西半球分界线上的点是()A.F点B.图中E点的经纬度是东经120度,北纬40度C.图中 2020-04-23 …
如图,已知在△ABC中,∠ACB=90°,AC=BC,直线MN过C点,AD⊥MN于D点,BE⊥MN 2020-05-16 …
如图所示是某小球从静止出发沿直线运动过程的频闪照片.O点是小球出发点,依次的A、B、C、D、E点是 2020-06-12 …
读图,完成相关问题。(12分)(1)此图反映的地区,图中所有经线会集的点E叫,图中用线所绘的纬线叫 2020-06-25 …
请据图回答:(1)图2中e点与d点相比较,e点时叶肉细胞中C3的含量;e点与f点相比较,e点时叶肉 2020-07-09 …
(9分)请据图回答:(1)图2中e点与d点相比较,e点时叶肉细胞中C3的含量;e点与f点相比较,e 2020-07-09 …
如图,在正方形ABCD中,E是正方形内一点,连接ED、EC、EB,(1)在图中画出△EDC绕着点C逆 2020-11-06 …
如图为地球的日照图,认真读图,完成有关问题:(1)在图中的相应地方分别用符号标出北极点与南极点.(2 2020-11-13 …
第一道:在正方形ABCD中,E点和F点是正方形的边BC和CD上一点,连接AE和AF,再连接EF,已知 2020-12-28 …