在路边安装路灯，灯柱AB与地面垂直，灯杆BC与灯柱AB所在平面与路面垂直，且∠ABC=120°，路灯采用锥形灯罩，射出的光线如图中的阴影部分所示，∠ACD=60°，AD=24米，∠ACB=θ（30°≤θ≤45°）

Question

在路边安装路灯，灯柱AB与地面垂直，灯杆BC与灯柱AB所在平面与路面垂直，且∠ABC=120°，路灯采用锥形灯罩，射出的光线如图中的阴影部分所示，∠ACD=60°，AD=24米，∠ACB=θ（30°≤θ≤45°）．

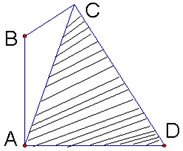
（Ⅰ）求灯柱AB的高度（用ξ表示）；
（Ⅱ）求灯柱AB与灯杆BC长度之和的最小值，及取最小值时θ的值．

Answer 1

（Ⅰ）∵∠ABC=120°，∠ACB=θ，∴∠BAC=60°-θ，
∵∠BAD=90°，∴∠CAD=30°+θ，
∵∠ACD=60°，∴∠ADC=90°-θ，
在△ACD中，∵(AD)/(sin∠ACD)=(AC)/(sin∠ADC)，∴AC=(24cosθ)/(sin60°)=16√(3)cosθ，
在△ABC中，∵(AB)/(sin∠ACB)=(AC)/(sinB)，∴AB=(ACsinθ)/(sin120°)=(16√(3)sinθcosθ)/(sin120°)=16sin2θ，
即灯柱AB的高度为16sin2θ米．…（6分）
（Ⅱ）在△ABC中，∵(BC)/(sin∠BAC)=(AC)/(sinB)，
∴BC=(ACsin(60°-θ))/(sin120°)=32cosθsin(60°-θ)=8√(3)+8√(3)cos2θ-8sin2θ，
即AB+BC=8√(3)+8√(3)cos2θ+8sin2θ=8√(3)+16sin(2θ+60°)，
∵30°≤θ≤45°，∴120°≤2θ+60°≤150°，
∴当θ=45°时，灯柱AB与灯杆BC长度之和的最小值为8√(3)+8米．…（12分）