两条平行光滑金属导轨足够长，其水平部分存在着竖直向上的匀强磁场，磁感应强度B=2T，导轨间距离L=0.5m，导轨倾斜部分与水平面夹角θ=30°，顶端所接电阻R=5Ω，现有一质量为m=1kg，接入导

Question

两条平行光滑金属导轨足够长，其水平部分存在着竖直向上的匀强磁场，磁感应强度B=2T，导轨间距离L=0.5m，导轨倾斜部分与水平面夹角θ=30°，顶端所接电阻R=5Ω，现有一质量为m=1kg，接入导轨间电阻r=3Ω的金属棒水平横放在导轨距水平面高度h=0.2m处，由静止释放（不计导轨电阻，不计金属棒滑动时在导轨弯折处的能量损失），求：

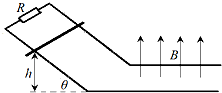
（1）金属棒在导轨水平部分滑动时加速度的最大值a_m；
（2）金属棒在水平导轨上做什么运动，并求出在整个运动过程中电阻R中产生的热量；
（3）当金属棒沿水平导轨运动位移为x=8m时，金属棒两端的电势差．

Answer 1

（1）金属棒在斜面上下滑时，有 mgh=(1)/(2)m

v

2 0

，得 v₀=√(2gh)
金属棒刚进入磁场时加速度最大，此时金属棒产生的感应电动势为 E=BLv
感应电流为 I=(E)/(R+r)
所受的安培力 F=BIL
根据牛顿第二定律得：F=ma_m；
联立得：a_m=(B2L2√(2gh))/((R+r)m)
代入解得 a_m=0.25m/s²；
（2）金属棒进入水平轨道时，受到向左的安培力作用而做减速运动，最终停止运动．
根据能量守恒得：
  Q_总=(1)/(2)m

v

2 0

=mgh=1×10×0.2J=2J
电阻R中产生的热量 Q_R=(R)/(R+r)Q_总=(5)/(5+3)×2J=1.25J
（3）设金属棒沿水平导轨运动速度为v时瞬时加速度为a，则由牛顿第二定律得
   (B2L2v)/(R+r)=ma
又 a=(△v)/(△t)
联立得：(B2L2v)/(R+r)=m(△v)/(△t)
得：(B2L2v)/(R+r)△t=m△v
而v△t=△x
两边求和得：

(B2L2△x)/(R+r)=

m△v
即得 (B2L2x)/(R+r)=mv₀-mv
解得 v=1m/s
金属棒两端的电势差 U=(R)/(R+r)E=(R)/(R+r)BLv=

作业帮用户 2017-01-09 举报

问题解析

（1）当金属棒进入水平轨道时，受到向左的安培力作用而减速，产生的感应电流减小，受到的安培力减小，加速度最小，所以金属棒刚进入磁场时加速度最大，先求出感应电流，再由牛顿第二定律求最大加速度．
（2）金属棒在水平导轨上做减速运动，最终停止运动，由能量守恒定律求R上产生的热量．
（3）根据牛顿第二定律、加速度的定义式，运用微元法求出金属棒运动x=8m位移时的速度，再由E=BLv和欧姆定律求金属棒两端的电势差．

名师点评

本题考点：

导体切割磁感线时的感应电动势 电磁感应中的能量转化

考点点评：

本题是电磁感应与电路知识的综合，掌握法拉第电磁感应定律、欧姆定律和能量守恒定律就可正确求解．在求解有关热量的问题，往往有两种选择：一是焦耳定律；二是能量守恒定律，对于电流是变化的情形，应根据能量守恒定律求解．

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议