羚羊从静止开始奔跑，经过距离能加速到最大速度，并能维持一段较长的时间；猎豹从静止开始奔路，经过的距离能加速到最大速度，以后只能维持这个速度4.0s，设猎豹距离

Question

羚羊从静止开始奔跑，经过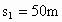 距离能加速到最大速度 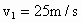，并能维持一段较长的时间；猎豹从静止开始奔路，经过 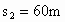的距离能加速到最大速度 ，以后只能维持这个速度4 . 0s，设猎豹距离羚羊x时开始攻击，羚羊则在猎豹开始攻击后1 . 0s开始奔跑．假定羚羊和猎豹在加速阶段分别做匀加速运动，且均沿同一直线奔跑，求：

(1)猎豹要在达到最大速度且未减速前追到羚羊，x值应在什么范围?

(2)猎豹要在其加速阶段追上羚羊，x值应在什么范围?

Answer 1

解析：
(1)；(2) 　　本题的研究对象有两个：羚羊和猎豹，其中羚羊将先匀加速运动，后匀速运动，而猎豹的运动则先匀加速运动，后匀速运动4.0s后将减速．但由于两个研究对象的运动并无必然的内在联系，每一个运动过程也不一定都将出现．所以，猎豹追上羚羊时，羚羊在做什么运动(是正在加速，还是已经在做匀速运动)就成了解决问题的关键，这需要我们根据题意作进一步的探索． (1)猎豹在达到最大速度且尚未减速前追到羚羊，即猎豹的运动只能是先匀加速运动，后匀速运动．设猎豹在维持最大速度的时间t内追到羚羊，由题意知．现在我们首先探索的问题是当猎豹追到羚羊时，羚羊的运动情况如何?为此，我们可先分别求得羚羊和猎豹做匀加速运动的加速度和时间．羚羊做匀加速运动的加速度为 ． 羚羊做匀加速运动的时间为 而猎豹做匀加速运动的加速度为 猎豹做匀加速运动的时间为 ． ①若猎豹刚达到最大速度时追上，则羚羊只加速了 ，则有 ②若猎豹刚要减速时追上，则有 由此可知，x值应为 (2)羚羊刚要开始奔跑时，猎豹已追上 ， 由此可知，x值应为
提示：
分析解决两物体追及、相碰问题，应该首先在理解题意的基础上，认清两物体的运动关系(位移的关系，速度的关系问题，时间的关系等)，必要时画出运动关联示意图．此类问题的特殊之处在于常与数值条件和临界条件相联系，找出相关联的临界方程的临界方程或用数学法找出相关的临界值是解决此类问题的关键和突破口．