早教吧作业答案频道 -->数学-->
四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.(1)若点O在四边形ABCD的内部,①如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE=°;②如图2,试探索∠B
题目详情
四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.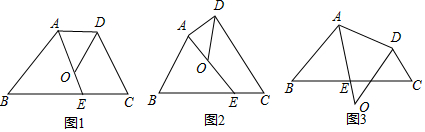
(1)若点O在四边形ABCD的内部,
①如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE=___°;
②如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.

(1)若点O在四边形ABCD的内部,
①如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE=___°;
②如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
▼优质解答
答案和解析
(1)①∵AD∥BC,∠B=40°,∠C=70°,
∴∠BAD=140°,∠ADC=110°,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAE=70°,∠ODC=55°,
∴∠AEC=110°,
∴∠DOE=360°-110°-70°-55°=125°;
故答案为:125;
②∠B+∠C+2∠DOE=360°,
理由:∵∠DOE=∠OAD+∠ADO,
∵AE、DO分别平分∠BAD、∠CDA,
∴2∠DOE=∠BAD+∠ADC,
∵∠B+∠C+∠BAD+∠ADC=360°,
∴∠B+∠C+2∠DOE=360°;
(2)∠B+∠C=2∠DOE,
理由:∵∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAD=2∠EAD,∠ADC=2∠ADO,
∴∠BAD+∠ADC=2(∠EAD+∠ADO),
∴360°-∠B-∠C=2(180°-∠DOE),
∴∠B+∠C=2∠DOE.
∴∠BAD=140°,∠ADC=110°,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAE=70°,∠ODC=55°,
∴∠AEC=110°,
∴∠DOE=360°-110°-70°-55°=125°;
故答案为:125;
②∠B+∠C+2∠DOE=360°,
理由:∵∠DOE=∠OAD+∠ADO,
∵AE、DO分别平分∠BAD、∠CDA,
∴2∠DOE=∠BAD+∠ADC,
∵∠B+∠C+∠BAD+∠ADC=360°,
∴∠B+∠C+2∠DOE=360°;
(2)∠B+∠C=2∠DOE,
理由:∵∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAD=2∠EAD,∠ADC=2∠ADO,
∴∠BAD+∠ADC=2(∠EAD+∠ADO),
∴360°-∠B-∠C=2(180°-∠DOE),
∴∠B+∠C=2∠DOE.
看了四边形ABCD中,∠BAD的角...的网友还看了以下:
从A到B是580米的下坡路,从B到C是260米的平路.甲、乙两人分别从A和C两地同时出发,相向而行 2020-04-07 …
读图,完成下列问题.(1)内蒙古自治区位于我国的(四大地理区域)地区,图中所示山脉是,它的东侧是我 2020-05-13 …
人体的体温之所以维持稳定,依赖于机体产热和散热的平衡.人体在夏季高温环境中,热量散出的主要途径为( 2020-06-14 …
食盐是我们必不可少的调味品.现在市场上有一种健康平衡盐,适量食用可维持人体Na+、K+等重要离子的 2020-06-23 …
证明:四个连续整数的积加上1是一个整数的平方. 2020-06-27 …
证明:四个连续整数的积加上1是一个整数的平方. 2020-06-27 …
已知3a2+2b2=5,求y=(2a2+1)(b2+2)最大值那个2a2是2a的平方...要用高二 2020-07-09 …
如图所示,匀强电场中有一直角三角形ABC,∠ABC=30°,BC=20cm.已知电场线的方向平行于 2020-07-10 …
人与人之间的平等以的平等为基础,体现为人格的平等何各项基本权利的平等. 2020-07-12 …
如图所示,半径为R=0.45m的光滑的14圆弧轨道AB与粗糙平面BC相连,质量m=1kg的物块由静 2020-07-13 …