早教吧作业答案频道 -->数学-->
问题在△ABC中,AC=BC,∠ACB=90°,点E在直线BC上(B,C除外),分别经过点E和点B做AE和AB的垂线,两条垂线交于点F,研究AE和EF的数量关系.探究发现某数学兴趣小组在探究AE,EF的关
题目详情
【问题】
在△ABC中,AC=BC,∠ACB=90°,点E在直线BC上(B,C除外),分别经过点E和点B做AE和AB的垂线,两条垂线交于点F,研究AE和EF的数量关系.
【探究发现】
某数学兴趣小组在探究AE,EF的关系时,运用“从特殊到一般”的数学思想,他们发现当点E是BC的中点时,只需要取AC边的中点G(如图1),通过推理证明就可以得到AE和EF的数量关系,请你按照这种思路直接写出AE和EF的数量关系;
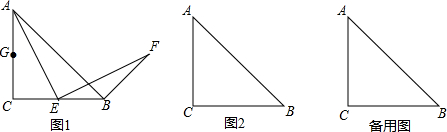
【数学思考】
那么当点E是直线BC上(B,C除外)(其它条件不变),上面得到的结论是否仍然成立呢?请你从“点E在线段BC上”;“点E在线段BC的延长线”;“点E在线段BC的反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明你的结论.
在△ABC中,AC=BC,∠ACB=90°,点E在直线BC上(B,C除外),分别经过点E和点B做AE和AB的垂线,两条垂线交于点F,研究AE和EF的数量关系.
【探究发现】
某数学兴趣小组在探究AE,EF的关系时,运用“从特殊到一般”的数学思想,他们发现当点E是BC的中点时,只需要取AC边的中点G(如图1),通过推理证明就可以得到AE和EF的数量关系,请你按照这种思路直接写出AE和EF的数量关系;

【数学思考】
那么当点E是直线BC上(B,C除外)(其它条件不变),上面得到的结论是否仍然成立呢?请你从“点E在线段BC上”;“点E在线段BC的延长线”;“点E在线段BC的反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明你的结论.
▼优质解答
答案和解析
【探究发现】AE和EF的数量关系为:AE=EF.
理由:如图1,取AC边的中点G,连接EG,
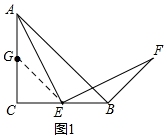
∵△ABC中,AC=BC,∠ACB=90°,
∴∠ABC=45°,AG=BE,△CEG是等腰直角三角形,
∴∠CGE=45°,∠EGA=135°,
∵AE⊥EF,AB⊥BF,
∴∠EBF=135°,∠EAG=∠FEB,
在△EAG和△FEB中,
,
∴△EAG≌△FEB(ASA),
∴AE=EF;
【数学思考】AE=EF仍然成立.
证明:①如图2,若点E在线段BC上,在AC上截取CG=CE,连接GE.
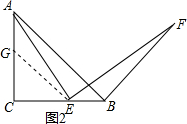
∵∠ACB=90°,
∴∠CGE=∠CEG=45°,
∵AE⊥EF,AB⊥BF,
∴∠AEF=∠ABF=∠ACB=90°,
∴∠FEB+∠AEF=∠AEB=∠EAC+∠ACB,
∴∠FEB=∠EAC,
∵CA=CB,
∴AG=BE,∠CBA=∠CAB=45°,
∴∠AGE=∠EBF=135°,
在△EAG和△FEB中,
,
∴△EAG≌△FEB(ASA),
∴AE=EF;
②如图3,若点E在线段BC的反向延长线上,在AC反向延长线上截取CG=CE,连接GE.
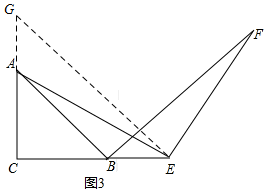
∵∠ACB=90°,
∴∠CGE=∠CEG=45°,
∵AE⊥EF,AB⊥BF,
∴∠AEF=∠ABF=∠ACB=90°,
∵∠FEB=∠AEF+∠AEC,∠EAG=∠C+∠AEC,
∴∠FEB=∠EAG,
∵CA=CB,
∴AG=BE,∠CBA=∠CAB=45°,
∴∠AGE=∠EBF=45°,
在△EAG和△FEB中,
,
∴△EAG≌△FEB(ASA),
∴AE=EF;
③如图4,若点E在线段BC的延长线,在AC延长线上截取CG=CE,连接GE.
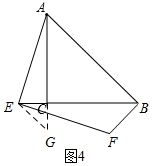
∵∠ACB=90°,
∴∠CGE=45°,∠ABC=45°,
∵AE⊥EF,AB⊥BF,
∴∠AEF=∠ABF=90°,
∴∠FEB+∠AEB=90°=∠EAG+∠AEB,∠EBF=45°=∠G,
∴∠FEB=∠EAG,
∵CA=CB,
∴AG=BE,
在△EAG和△FEB中,
,
∴△EAG≌△FEB(ASA),
∴AE=EF.
理由:如图1,取AC边的中点G,连接EG,

∵△ABC中,AC=BC,∠ACB=90°,
∴∠ABC=45°,AG=BE,△CEG是等腰直角三角形,
∴∠CGE=45°,∠EGA=135°,
∵AE⊥EF,AB⊥BF,
∴∠EBF=135°,∠EAG=∠FEB,
在△EAG和△FEB中,
|
∴△EAG≌△FEB(ASA),
∴AE=EF;
【数学思考】AE=EF仍然成立.
证明:①如图2,若点E在线段BC上,在AC上截取CG=CE,连接GE.

∵∠ACB=90°,
∴∠CGE=∠CEG=45°,
∵AE⊥EF,AB⊥BF,
∴∠AEF=∠ABF=∠ACB=90°,
∴∠FEB+∠AEF=∠AEB=∠EAC+∠ACB,
∴∠FEB=∠EAC,
∵CA=CB,
∴AG=BE,∠CBA=∠CAB=45°,
∴∠AGE=∠EBF=135°,
在△EAG和△FEB中,
|
∴△EAG≌△FEB(ASA),
∴AE=EF;
②如图3,若点E在线段BC的反向延长线上,在AC反向延长线上截取CG=CE,连接GE.

∵∠ACB=90°,
∴∠CGE=∠CEG=45°,
∵AE⊥EF,AB⊥BF,
∴∠AEF=∠ABF=∠ACB=90°,
∵∠FEB=∠AEF+∠AEC,∠EAG=∠C+∠AEC,
∴∠FEB=∠EAG,
∵CA=CB,
∴AG=BE,∠CBA=∠CAB=45°,
∴∠AGE=∠EBF=45°,
在△EAG和△FEB中,
|
∴△EAG≌△FEB(ASA),
∴AE=EF;
③如图4,若点E在线段BC的延长线,在AC延长线上截取CG=CE,连接GE.

∵∠ACB=90°,
∴∠CGE=45°,∠ABC=45°,
∵AE⊥EF,AB⊥BF,
∴∠AEF=∠ABF=90°,
∴∠FEB+∠AEB=90°=∠EAG+∠AEB,∠EBF=45°=∠G,
∴∠FEB=∠EAG,
∵CA=CB,
∴AG=BE,
在△EAG和△FEB中,
|
∴△EAG≌△FEB(ASA),
∴AE=EF.
看了问题在△ABC中,AC=BC,...的网友还看了以下:
现有A、B、C、D、E、F六种短周期元素,它们的原子序数依次增大.①A、D同主族,C与E同主族,D 2020-04-08 …
(12分)A、B、C、D、E是五种短周期元素。已知:它们的原子序数依次增大,A是元素周期表中原子半 2020-04-08 …
A、B、C、D、E为原子序数依次递增的5种短周期元素,已知:①A、B、C同周期,C、E同主族②A原 2020-04-08 …
A、B、C、D、E、F六种元素,其中ABCDE为短周期元素,①原子半径A<C<B<E<D②原子最外 2020-05-13 …
A、B、C、D是四种短周期元素,E、F是过渡元素.A、B、C同周期,C、D同主族,A的原子结构示意 2020-05-14 …
慢性宫颈炎的典型临床表现是A:白带增多B:外阴疼痛C:外阴瘙痒D:外阴湿疹E:外阴灼热感 2020-06-07 …
现有A,B,C,D,E,F,G七种短周期主族元素,原子序数依次增大.已知A与D,C与F分别同主族, 2020-07-07 …
周期表前四周期的元素a、b、c、d、e,原子序数依次增大.A的核外电子总数与其周期数相同,b的价电子 2020-11-01 …
现有原子序数之和为51的五种短周期元素A,B,C,D,E。已知A单质在常温下为无色气体;B原子的最外 2020-11-17 …
生产某种产品100t,需用A种原料200t,或B种原料200.5t,或C种原料195.5t,或D种原 2020-11-21 …