早教吧作业答案频道 -->数学-->
如图,已知∠AOB=a外有一点P,画点P关于直线OA的对称点P′,再作点P′关于直线OB的对称点P″.(1)试猜想∠POP″与a的大小关系,并说出你的理由.(2)当P为∠AOB内一点或∠AOB边上一点
题目详情
如图,已知∠AOB=a外有一点P,画点P关于直线OA的对称点P′,再作点P′关于直线OB的对称点P″.
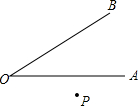
(1)试猜想∠POP″与a的大小关系,并说出你的理由.
(2)当P为∠AOB 内一点或∠AOB边上一点时,上述结论是否成立?

(1)试猜想∠POP″与a的大小关系,并说出你的理由.
(2)当P为∠AOB 内一点或∠AOB边上一点时,上述结论是否成立?
▼优质解答
答案和解析
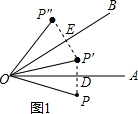 (1)猜想:∠POP″=2α.
(1)猜想:∠POP″=2α.
理由:如图1,在△DOP′与△DOP中
∵
,
∴△DOP′≌△DOP.
同理可得,△EOP″≌△EOP′
∴∠POP″=2α;
(2)成立.
如图2,当点P在∠AOB内时,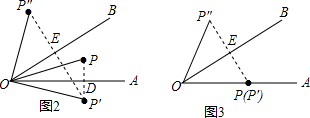
∵同(1)可得,
△DOP′≌△DOP,EOP″≌△EOP′,
∴∠POD=∠P′OD,∠EOP″=∠EOP′,
∴∠POP″=∠P′OP″-∠POP′=3α-α=2α.
如图3,当点P在∠AOB的边上时,
∵同(1)可得△EOP″≌△EOP,
∴∠POP″=2α.
 (1)猜想:∠POP″=2α.
(1)猜想:∠POP″=2α.理由:如图1,在△DOP′与△DOP中
∵
|
∴△DOP′≌△DOP.
同理可得,△EOP″≌△EOP′
∴∠POP″=2α;
(2)成立.
如图2,当点P在∠AOB内时,

∵同(1)可得,
△DOP′≌△DOP,EOP″≌△EOP′,
∴∠POD=∠P′OD,∠EOP″=∠EOP′,
∴∠POP″=∠P′OP″-∠POP′=3α-α=2α.
如图3,当点P在∠AOB的边上时,
∵同(1)可得△EOP″≌△EOP,
∴∠POP″=2α.
看了如图,已知∠AOB=a外有一点...的网友还看了以下:
高一物理题在电场中的P点放一电荷量为4×10-9C的点电荷,它受到的电场力为2×10-5N,则P点 2020-05-13 …
电荷量为-2.0×10-16C的点电荷,在电场中P点具有-6.0×10-16J的电势能,P点的电势 2020-05-13 …
电场中有一点P,下列说法中正确的有()A.若放在P点的电荷的电荷量减半,则P点的场强减半B.若放在 2020-05-15 …
电场中有一点P,下列说法正确的是()A.若放在P点的电荷的电量减半,则P点场强减半B.若P点没有检 2020-05-20 …
已知圆M的方程为x^2+(y-2)^2=1,直线l的方程为x-2y=0,点P在直线l上,过P点作圆 2020-06-14 …
电场中有一点P,下列说法中正确的是A.若放在P点的电荷的电量减半,则P点处的电场强度减半B.若P点 2020-07-23 …
已知:点P(2m+4,m-1).试分别根据下列条件,求出P点的坐标.(1)点P在y轴上;(2)点P 2020-07-30 …
一质点做直线运动经过p点的速度为3米每秒则下列说法正确的是A、过P点后的1s内质点的位移是3mB、 2020-07-31 …
如图,以M(3,3)为圆心的⊙M与y轴相切于点D,x轴上一点A(23,0),点P从A点出发,沿x轴 2020-07-31 …
平面直角坐标系若点P(x,y)在x轴上方,|x|=5,|y|=4,则P点的坐标为点P(x,y),若x 2020-11-01 …