（根据2013年高考冲刺卷改编）函数，其中(1)当m=n+6时，函数f(x)有两个极值点.求n的取值范围;求.（2），若函数f(x)g(x)在区间上分别为单调递增和递减函数，求n-m的最大值.
（根据2013年高考冲刺卷改编）函数
，其中
(1)当m=n+6时，函数f(x)有两个极值点
.
求n的取值范围;
求
.
（2）
，若函数f(x) g(x)在区间
上分别为单调递增和递减函数，求n-m的最大值.
当m=n+6时，
则
，由
又由于
所以函数应满足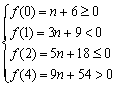
即
-
-
由于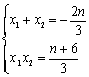
，代入上式得
设
，
又因为
则
的取值范围为
-
（2）
，则
若
-
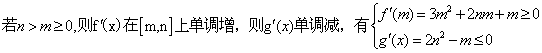
从而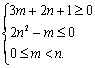
有线性规划可得
f(m)+f(n)=f(m+n),f(1005)=2,求f(2)+f(4)+f(6)+.f(2008 2020-03-30 …
,;定义在正整数集f(x)对任意m,n,都有f(m+n)=f(m)+f(n)+4(m+n)-2,且 2020-05-13 …
Y=x^2/(1+x^2),n∈Z+,则f(1)+f(2)+f(3)+...+f(n)+f(1/2 2020-05-13 …
已知2^m=3,32^n=6,求2^3m-10n 2020-05-17 …
已知2^m=a,32^n=b,求2^3m+10n的值 求的是2的3m+10n次方 2020-05-17 …
已知函数y=f(n),f(0)=2,且满足f(n)=f(n-1)/(n+1),n属于N+,求f(1 2020-06-02 …
1,计算:-2^100*0.5^100*(-1)^2003-1/22,已知2^m=3,2^n=4, 2020-07-22 …
斐波那契数列解法中的一个问题求解?这是解法裴波那契数列：1,1,2,3,5,8,13,.裴波那契数 2020-07-23 …
整式的计算.1.已知a^3n=5b^2n=3求a^6nb^4n的值2.设n为正整数且x^2n=2求 2020-07-30 …
已知：2^m=3,32^n=6.求2^2m-10m的值x^2-2x当x=1,y=-2时,求分式的值2 2020-11-01 …