某工厂打算建造如图所示的圆柱形容器（不计厚度，长度单位：米），按照设计要求，该容器的底面半径为r，高为h，体积为16π立方米，且h≥2r．已知圆柱的侧面部分每平方米建造费用为3千

Question

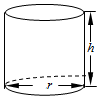
某工厂打算建造如图所示的圆柱形容器（不计厚度，长度单位：米），按照设计要求，该容器的底面半径为r，高为h，体积为16π立方米，且h≥2r．已知圆柱的侧面部分每平方米建造费用为3千元，圆柱的上、下底面部分每平方米建造费用为a千元，假设该容器的建造费用仅与其表面积有关，该容器的建造总费用为y千元．

（1）求y关于r的函数表达式，并求出函数的定义域；
（2）问r为多少时，该容器建造总费用最小？

Answer 1

（1）设容器的容积为V，
由题意知V=πr²h=16π，故h=(16)/(r2)，…..（2分）
因为h≥2r，所以0<r≤2，…．（4分）
故建造费用y=2πrh×3+2πr2a=6πr×(16)/(r2)+2πr2a，
即y=2πar2+(96π)/(r)，0<r≤2．…．（6分）
（2）由（1）得y′=4πar-(96π)/(r2)(0<r≤2)，
令y'=0得r=2

3

(3)/(a)

，…..（8分）
①当0<2

3

(3)/(a)

<2即a>3时，
若r∈(0，2

3

(3)/(a)

)，则y'<0，函数单调递减；
若r∈(2

3

(3)/(a)

，2)，则y'>0，函数单调递增；
所以r=2

3

(3)/(a)

时，函数取得极小值，也是最小值．…（12分）
②当2

3

(3)/(a)

≥2即0<a≤3时，
因为r∈（0，2]，则y'<0，函数单调递减；
则r=2时，函数取得最小值．…（14分）
综上所述：若a>3，当r=2

3

(3)/(a)

时，建造总费用最少；
若0<a≤3，当r=2时，建造总费用最少．…..（16分）