早教吧作业答案频道 -->数学-->
已知在△ABC中,AB=AC=8,BC=4,点P是边AC上的一个动点,∠APD=∠ABC,AD∥BC,联结DC.(1)如图1,如果DC∥AB,求AP的长;(2)如图2,如果直线DC与边BA的延长线交于点E,设AP=x,AE=y,求y
题目详情
已知在△ABC中,AB=AC=8,BC=4,点P是边AC上的一个动点,∠APD=∠ABC,AD∥BC,联结DC.
(1)如图1,如果DC∥AB,求AP的长;
(2)如图2,如果直线DC与边BA的延长线交于点E,设AP=x,AE=y,求y关于x的函数解析式,并写出它的定义域;
(3)如图3,如果直线DC与边BA的反向延长线交于点F,联结BP,当△CPD与△CBF相似时,试判断线段BP与线段CF的数量关系,并说明你的理由.
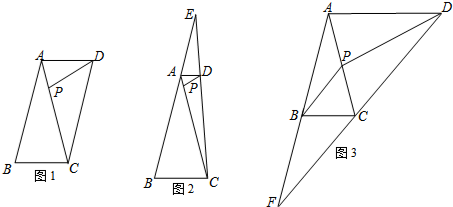
(1)如图1,如果DC∥AB,求AP的长;
(2)如图2,如果直线DC与边BA的延长线交于点E,设AP=x,AE=y,求y关于x的函数解析式,并写出它的定义域;
(3)如图3,如果直线DC与边BA的反向延长线交于点F,联结BP,当△CPD与△CBF相似时,试判断线段BP与线段CF的数量关系,并说明你的理由.

▼优质解答
答案和解析
考点:
相似形综合题
专题:
分析:
(1)先证明△DPA∽△ABC,得出比例式APBC=ADAC,即可求出AP=2;(2)由(1)得出APBC=ADAC,AD=2AP,再由AD∥BC,得出ADBC=AEED,即可得出y=8x2-x;(3)由△CPD∽△CBF,得出PDBF=CPBC,得出2xy=8-x4①,再由AD∥BC,得BCAD=BFAF,得出42x=yy+8②,由①②解得x、y的值,得出BP是△ACF的中位线,即可得出结论:BP=12CF.
(1)∵AD∥BC,∴∠DAP=∠ACB,∵∠APD=∠ABC,∴△DPA∽△ABC,∴APBC=ADAC,∵四边形ABCD是平行四边形,∴AD=BC=4,∵AB=AC=8,∴AP4=48,∴AP=2;(2)由(1)得,APBC=ADAC,∴AD=2AP,∵AD∥BC,∴ADBC=AEED,∵AP=x,AE=y,∴AD=2x,EB=y+8,∴2x4=yy+8,∴y=8x2-x,它的定义域是0<x<2;(3)BP=12CF;∵∠APD=∠ABC,∴∠DPC=∠FBC,∵∠PCD>∠F,又△CPD与△CBF相似,∴∠PCD=∠BCE,∴△CPD∽△CBF,∴PDBF=CPBC,∵AB=AC,∴∠ABC=∠ACB,∵∠APD=∠ABC,∠DAP=∠ACB,∴∠DAP=∠APD,∴AD=PD,设AP=x,BF=y,则AD=PD=2x,AF=y+8,∴2xy=8-x4①,∵AD∥BC,∴BCAD=BFAF,∴42x=yy+8②,由①②得:x=4,y=8,∴AP=PC=4,AB=BF=8,∴BP是△ACF的中位线,∴BP=12CF.
点评:
本题考查了相似三角形的判定与性质、平行线四边形的性质、三角形的中位线以及函数解析式的求法;证明三角形相似得出比例式是解决问题的关键.
考点:
相似形综合题
专题:
分析:
(1)先证明△DPA∽△ABC,得出比例式APBC=ADAC,即可求出AP=2;(2)由(1)得出APBC=ADAC,AD=2AP,再由AD∥BC,得出ADBC=AEED,即可得出y=8x2-x;(3)由△CPD∽△CBF,得出PDBF=CPBC,得出2xy=8-x4①,再由AD∥BC,得BCAD=BFAF,得出42x=yy+8②,由①②解得x、y的值,得出BP是△ACF的中位线,即可得出结论:BP=12CF.
(1)∵AD∥BC,∴∠DAP=∠ACB,∵∠APD=∠ABC,∴△DPA∽△ABC,∴APBC=ADAC,∵四边形ABCD是平行四边形,∴AD=BC=4,∵AB=AC=8,∴AP4=48,∴AP=2;(2)由(1)得,APBC=ADAC,∴AD=2AP,∵AD∥BC,∴ADBC=AEED,∵AP=x,AE=y,∴AD=2x,EB=y+8,∴2x4=yy+8,∴y=8x2-x,它的定义域是0<x<2;(3)BP=12CF;∵∠APD=∠ABC,∴∠DPC=∠FBC,∵∠PCD>∠F,又△CPD与△CBF相似,∴∠PCD=∠BCE,∴△CPD∽△CBF,∴PDBF=CPBC,∵AB=AC,∴∠ABC=∠ACB,∵∠APD=∠ABC,∠DAP=∠ACB,∴∠DAP=∠APD,∴AD=PD,设AP=x,BF=y,则AD=PD=2x,AF=y+8,∴2xy=8-x4①,∵AD∥BC,∴BCAD=BFAF,∴42x=yy+8②,由①②得:x=4,y=8,∴AP=PC=4,AB=BF=8,∴BP是△ACF的中位线,∴BP=12CF.
点评:
本题考查了相似三角形的判定与性质、平行线四边形的性质、三角形的中位线以及函数解析式的求法;证明三角形相似得出比例式是解决问题的关键.
看了已知在△ABC中,AB=AC=...的网友还看了以下:
如果A=a+3b的a-2b+3次方根为a+3b的算术平方根,B=1-a平方的2a-b-1次方根为1 2020-05-15 …
如-a,1-a,a和a+1四个数在数轴上所对应的点是按从左到右的顺序排列的,那么A.a>0B.a1 2020-06-04 …
如表是元素周期表的一部分,针对所给的元素,完成下列各小题.主族周期ⅠAⅡAⅢAⅣAⅤAⅥAⅦA2C 2020-06-09 …
阅读材料,解答下列问题.例:当a>0时,如a=6,则|a|=|6|=6,故此时|a|是它本身;当a 2020-06-21 …
根据绝对值得定义,回答下面的问题,1:如果|a|分之a等于1,那么a0;2:如果|a|分之a等于- 2020-08-01 …
(2013•随州)如图A是实验室制取二氧化碳并检验其性质的实验装置图,请你回答:(1)a仪器的名称为 2020-11-12 …
用">""<"或"="号填空如果a小于0,b大于0,那么a*b0,a分之b0.如果a大于0,b小于0 2020-12-17 …
如果a、b是有理数,则下列各式子成立的是()A.如果a<0,b<0,那么a+b>0B.如果a>0,b 2021-02-02 …
如果a表示有理数,那么下列说法中,错误的是()A.若a=-5,则-a=5B.若a=-a,则a=0C. 2021-02-02 …
7、如果a表示有理数,那么下列说法中,错误的是()A、若a=-5,则-a=5B、若a=-a,则a=0 2021-02-02 …