早教吧作业答案频道 -->数学-->
过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.(Ⅰ)求证:A、F、B、P四点共圆.(Ⅱ)求证:BE平分线段CD.
题目详情
过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.
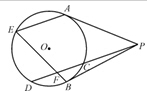
(Ⅰ)求证:A、F、B、P四点共圆.
(Ⅱ)求证:BE平分线段CD.

(Ⅰ)求证:A、F、B、P四点共圆.
(Ⅱ)求证:BE平分线段CD.
▼优质解答
答案和解析
证明:(Ⅰ)∵AE∥CD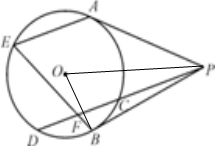
∴∠PFB=∠AEB
又PA,PB均 O的切线
故OP平分
,由圆周角定理和圆心圆定理可得∠POB=∠AEB
∴∠PFB=∠POB
由四点共圆判定定理的推论可得O,F,B,P四点共圆,
∵O,A,B,P四点共圆,
∴A、F、B、P四点共圆.
(Ⅱ)由PB为圆O的切线,OB为过切点的半径
可得∠OBP=90°
再由同弧或等弧所对的圆周角相等可得∠OFP=90°
再由垂径定理可得CF=DF,
∴BE平分线段CD.

∴∠PFB=∠AEB
又PA,PB均 O的切线
故OP平分
 |
| AB |
∴∠PFB=∠POB
由四点共圆判定定理的推论可得O,F,B,P四点共圆,
∵O,A,B,P四点共圆,
∴A、F、B、P四点共圆.
(Ⅱ)由PB为圆O的切线,OB为过切点的半径
可得∠OBP=90°
再由同弧或等弧所对的圆周角相等可得∠OFP=90°
再由垂径定理可得CF=DF,
∴BE平分线段CD.
看了过圆O外一点P向圆引两条切线P...的网友还看了以下:
一个圆柱体,若要两底面圆心的连线切开,切开恰好是边长6厘米的正方形,这个切面的面积是多少?这个圆柱 2020-05-17 …
只适用于轻载连接的键是( )。A.平键B.半圆键C.楔向键D.切向键 2020-05-18 …
停用保护连接片使用术语为( ) ( A )停用 ( B )退出 ( C )切除 ( D )切 2020-05-31 …
各种保护连接片、切换把手、按钮均应标明( )。 A.名称 B.编号 C.用途 D.切换方向 2020-05-31 …
依如图有关基因工程的工具酶功能的叙述,不正确的是()A.切断a处的酶为限制性核酸内切酶B.连接a处 2020-06-05 …
f(x)在的某邻域内连续,切limx趋于0f(x)/x(1-cosx)=-1,证明x=0是驻点但不 2020-07-08 …
为了观察小狗甲状腺功能亢进引起的病变,在下列各项实验措施中,宜采取的是A.用甲状腺制剂连续饲喂发育 2020-07-10 …
直线和椭圆相切,连接切点和两焦点,他们的连线和直线构成的两个夹角为啥相等,这是啥性质? 2020-07-31 …
一个圆柱体,如果沿俩底面圆心的连线切开,切面恰好是边长4厘米的正方形,这一个切面的面积是多少?这个 2020-07-31 …
一种质粒和人的胰岛素基因存在的限制酶的酶切位点(用E1表示)如图所示,a表示标记基因,b表示胰岛素基 2020-10-31 …