有一块半径为R（R为正常数）的半圆形空地，开发商计划征地建一个游泳池ABCD和其附属设施，附属设施占地形状是等腰△CDE，其中O为圆心，A，B在圆的直径上，C，D，E在半圆周上，如图．（

Question

有一块半径为R（R为正常数）的半圆形空地，开发商计划征地建一个游泳池ABCD和其附属设施，附属设施占地形状是等腰△CDE，其中O为圆心，A，B在圆的直径上，C，D，E在半圆周上，如图．

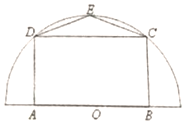
（1）设∠BOC=θ，征地面积为f（θ），求f（θ）的表达式，并写出定义域；
（2）当θ满足g（θ）=f（θ）+R²sinθ取得最大值时，开发效果最佳，求出开发效果最佳的角θ的值，并求出g（θ）的最大值．

Answer 1

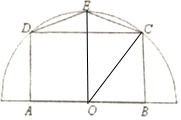（1）连结OE，OC，
在Rt△OBC中，BC=Rsinθ，OB=Rcosθ，
∴S_梯形OBCE=(1)/(2)（Rsinθ+R）Rcosθ=(1)/(2)R²（1+sinθ）cosθ，
∴f（θ）=2S_梯形OBCE=R²（1+sinθ）cosθ，θ∈（0，(π)/(2)）．
（2）g（θ）=R²（1+sinθ）cosθ+R²sinθ=R²（sinθ+cosθ+sinθcosθ），
令t=sinθ+cosθ=√(2)sin（θ+(π)/(4)），则t∈（1，√(2)]，sinθcosθ=(t2-1)/(2)，
∴g（θ）=R²（(t2-1)/(2)+t）=(R2)/(2)[（t+1）²-2]，
令h（t）=(R2)/(2)[（t+1）²-2]，则h（t）在（1，√(2)]上单调递增，
∴当t=√(2)即θ=(π)/(4)时，h（t）取得最大值（(1)/(2)+√(2)）R²，