早教吧作业答案频道 -->数学-->
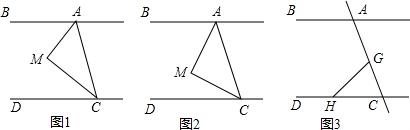
(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系并说明理由;(2)如图2,当∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD
题目详情
(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,G为线段AC上一定点,点H为直线CD上一动点且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外)∠CGH+∠CHG与∠BAC有何数量关系?猜想结论并说明理由.
(2)如图2,当∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,G为线段AC上一定点,点H为直线CD上一动点且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外)∠CGH+∠CHG与∠BAC有何数量关系?猜想结论并说明理由.

▼优质解答
答案和解析
(1)∵CM平分∠ACD,AM平分∠BAC,
∴∠BAC=2∠MAC,∠ACD=2∠ACM,
∵∠MAC+∠ACM=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAM+∠MCD=90°;
理由:如图2,过M作MF∥AB,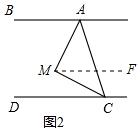
∵AB∥CD,
∴MF∥AB∥CD,
∴∠BAM=∠AMF,∠FMC=∠DCM,
∵∠M=90°,
∴∠BAM+∠MCD=90°;
(3)过点G作GP∥AB,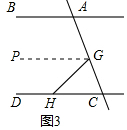
∵AB∥CD
∴GP∥CD,
∴∠BAC=∠PGC,∠CHG=∠PGH,
∴∠PGC=∠CHG+∠CGH,
∴∠BAC=∠CHG+∠CGH.
∴∠BAC=2∠MAC,∠ACD=2∠ACM,
∵∠MAC+∠ACM=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAM+∠MCD=90°;
理由:如图2,过M作MF∥AB,

∵AB∥CD,
∴MF∥AB∥CD,
∴∠BAM=∠AMF,∠FMC=∠DCM,
∵∠M=90°,
∴∠BAM+∠MCD=90°;
(3)过点G作GP∥AB,

∵AB∥CD
∴GP∥CD,
∴∠BAC=∠PGC,∠CHG=∠PGH,
∴∠PGC=∠CHG+∠CGH,
∴∠BAC=∠CHG+∠CGH.
看了 (1)如图1,CM平分∠AC...的网友还看了以下:
(2013•扬州一模)在△ABC中,∠A=90°,BC=10,tan∠ABC=3:4,M是AB上的 2020-05-13 …
一个数学综合题.Rt△ACB中,∠ACB=90°,AC=BC,M是AB的中点,D是AB上一动点.( 2020-05-21 …
如图(1),已知圆O是等边△ABC的外接圆,过O点作MN∥BC分别交AB、AC于M、N,且MN=a 2020-05-24 …
如图①,在△ABC中,∠ACB=90°,M为AC上任意一点(不与A,C重合),过M作直线MN交BC 2020-06-13 …
直线y=33x+3与x轴交于点A,与y轴交于点B,⊙M为△AOB的外接圆.点C是劣弧上一动点(不与 2020-06-23 …
如图①,在△ABC中,∠ACB=90°,M为AC上任意一点(不与A,C重合),过M作直线MN交BC 2020-07-21 …
(2014•夹江县二模)在△ABC中,∠A=90°,AB=8,AC=6,M是AB上的动点(不与A, 2020-07-22 …
在平面直角坐标系xOy中,半径为1的O与x轴负半轴交于点A,点M在O上,将点M绕点A顺时针旋转60° 2020-11-01 …
(2013•梧州一模)如图,将边长为4的正方形纸片ABCD折叠,使点B落在AD边上的M处(点M不与A 2020-11-13 …
抛物线与x轴交于A(-2,0)、B(6,0)两点,与y轴交于点C(0,-4)。(1)求抛物线的解析式 2021-01-10 …