早教吧作业答案频道 -->数学-->
如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.(1)当2θ=π3时,求圆Q的半径;(2)当θ为变量时,
题目详情
如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.
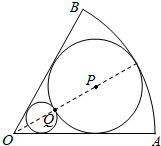
(1)当2θ=
时,求圆Q的半径;
(2)当θ为变量时,求圆Q的半径的最大值.

(1)当2θ=
| π |
| 3 |
(2)当θ为变量时,求圆Q的半径的最大值.
▼优质解答
答案和解析
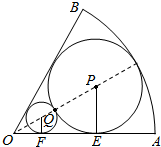 (1)设圆P的半径为x,圆Q的半径为y,
(1)设圆P的半径为x,圆Q的半径为y,
圆P切OA于E,连结PE,当2θ=
时,
则sin
=
=
,
∴x=
r.
同理,得sin
=
=
,解得:y=
,即圆Q的半径为
.
(2)∵sinθ=
,解得:x=
,
又∵sinθ=
,
∴解得:y=
.
令sinθ=t,0<t<1,y=r•
,
则y′=r•
,
令y′=0,则t=
,
0<t<
时,y′>0;
<t<1时,y′<0.
∴当t=
时,y极大值=ymax,
∴圆Q的半径的最大值为
,此时sinθ=
.
 (1)设圆P的半径为x,圆Q的半径为y,
(1)设圆P的半径为x,圆Q的半径为y,圆P切OA于E,连结PE,当2θ=
| π |
| 3 |
则sin
| π |
| 6 |
| 1 |
| 2 |
| x |
| r-x |
∴x=
| 1 |
| 3 |
同理,得sin
| π |
| 6 |
| 1 |
| 2 |
| y |
| r-2x-y |
| r |
| 9 |
| r |
| 9 |
(2)∵sinθ=
| x |
| r-x |
| rsinθ |
| 1+sinθ |
又∵sinθ=
| y |
| r-2x-y |
∴解得:y=
| rsinθ(1-sinθ) |
| (1+sinθ)2 |
令sinθ=t,0<t<1,y=r•
| t-t2 |
| (1+t)2 |
则y′=r•
| 1-3t |
| (1+t)3 |
令y′=0,则t=
| 1 |
| 3 |
0<t<
| 1 |
| 3 |
| 1 |
| 3 |
∴当t=
| 1 |
| 3 |
∴圆Q的半径的最大值为
| r |
| 8 |
| 1 |
| 3 |
看了 如图,在半径为常数r,圆心角...的网友还看了以下:
如图,AC是圆O的直径,PA切圆O于点A,点B是圆O上的一点,且角BAC等于三十度,角APB等于六 2020-04-12 …
如图.AB为圆o的直径.DE切圆o于D.AE垂直于DE于E.BF切圆o于B,交AD于F.(1)弧C 2020-04-25 …
1,在梯形ABCD中,AD平行于BC,角BCD=90°,以CD为直径的半圆O切AB于点E,已知这个 2020-05-14 …
如图,AB为圆O的直径,PB为O的切线,AC//OP,点C在圆O上,OP交圆O于D,DA交BC于G 2020-06-27 …
在Rt△ABC中,∠C=90°,AC=3,BC=4(1)求△ABC内切圆的半径(2)若移动圆心O的 2020-07-09 …
如图,AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,∠APB=60° 2020-07-14 …
如图,AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,BC=3,CD=2AB是⊙O的直径 2020-07-21 …
如图,已知⊙O与⊙O外离,AB、CD是内公切线,OO′=10,若⊙O的半径为2,⊙O′的半径为3. 2020-07-26 …
如图,O为正方形ABCD对角线上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.(1)求证: 2020-07-30 …
数学圆的切线1.如图,在三角形ABC中,角BCA=90度,角A=30度,以AB为直径画圆O,延长A 2020-07-31 …