早教吧作业答案频道 -->数学-->
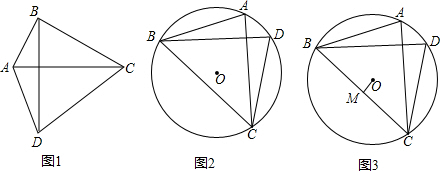
若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的
题目详情
若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)矩形___“奇妙四边形”(填“是”或“不是”);
(2)如图2,已知 O的内接四边形ABCD是“奇妙四边形”,若 O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;
(3)如图3,已知 O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
(1)矩形___“奇妙四边形”(填“是”或“不是”);
(2)如图2,已知 O的内接四边形ABCD是“奇妙四边形”,若 O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;
(3)如图3,已知 O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.

▼优质解答
答案和解析
 (1)矩形的对角线相等但不垂直,
(1)矩形的对角线相等但不垂直,
所以矩形不是“奇妙四边形”;
故答案为不是;
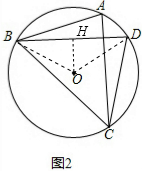
(2)连结OB、OD,作OH⊥BD于H,如图2,则BH=DH,
∵∠BOD=2∠BCD=2×60°=120°,
∴∠OBD=30°,
在Rt△OBH中,∵∠OBH=30°,
∴OH=
OB=3,
∴BH=
OH=3
,
∵BD=2BH=6
,
∴AC=BD=6
,
∴“奇妙四边形”ABCD的面积=
×6
×6
=54;
(3)OM=
AD.理由如下:
连结OB、OC、OA、OD,作OE⊥AD于E,如图3,
∵OE⊥AD,
∴AE=DE,
∵∠BOC=2∠BAC,
而∠BOC=2∠BOM,
∴∠BOM=∠BAC,
同理可得∠AOE=∠ABD,
∵BD⊥AC,
∴∠BAC+∠ABD=90°,
∴∠BOM+∠AOE=90°,
∵∠BOM+∠OBM=90°,
∴∠OBM=∠AOE,
在△BOM和△OAE中
,
∴△BOM≌△OAE,
∴OM=AE,
∴OM=
AD.
 (1)矩形的对角线相等但不垂直,
(1)矩形的对角线相等但不垂直,所以矩形不是“奇妙四边形”;
故答案为不是;
(2)连结OB、OD,作OH⊥BD于H,如图2,则BH=DH,
∵∠BOD=2∠BCD=2×60°=120°,
∴∠OBD=30°,
在Rt△OBH中,∵∠OBH=30°,
∴OH=
| 1 |
| 2 |
∴BH=
| 3 |
| 3 |
∵BD=2BH=6
| 3 |
∴AC=BD=6
| 3 |
∴“奇妙四边形”ABCD的面积=
| 1 |
| 2 |
| 3 |
| 3 |
(3)OM=
| 1 |
| 2 |
连结OB、OC、OA、OD,作OE⊥AD于E,如图3,

∵OE⊥AD,
∴AE=DE,
∵∠BOC=2∠BAC,
而∠BOC=2∠BOM,
∴∠BOM=∠BAC,
同理可得∠AOE=∠ABD,
∵BD⊥AC,
∴∠BAC+∠ABD=90°,
∴∠BOM+∠AOE=90°,
∵∠BOM+∠OBM=90°,
∴∠OBM=∠AOE,
在△BOM和△OAE中
|
∴△BOM≌△OAE,
∴OM=AE,
∴OM=
| 1 |
| 2 |
看了若一个四边形的两条对角线互相垂...的网友还看了以下:
对数据库数据的删除是由数据库管理系统的哪个功能模块实现的? A.数据库存取功能模块 B. 2020-05-23 …
(9)下列关于数据运算的叙述中,哪一条是不正确的? A)数据运算是数据结构的一个重要方面 B)数据运 2020-05-23 …
( 59 )下列关于数据库系统的叙述中,哪一个是不正确的?A )个人计算机系统上的单用户数据库系统一 2020-05-23 …
对数据库数据的删除是由数据库管理系统的哪个功能模块实现的?A.数据库存取功能模块B.数据库存储 2020-05-23 …
下列与数据元素有关的叙述中,哪一条是不正确的?A.数据元素是数据的基本单位,即数据集合中的个体B 2020-05-23 …
下列关于数据运算的叙述中,哪一条是不正确的?A.数据运算是数据结构的一个重要方面B.数据运算的具 2020-05-23 …
下列与数据元素有关的叙述中,哪一个是不正确的?()A.数据元素是数据的基本单位,即数据集合中的个 2020-05-23 …
下列关于数据的逻辑结构的叙述中,哪一个是正确的?()A.数据的逻辑结构是数据间关系的描述B.数据的 2020-05-24 …
下列关于数据结构的叙述中,哪一个是不正确的?A.数据的逻辑结构是数据间关系的描述B.数据的存储结 2020-05-24 …
10、有关信息和数据的说法中,是正确的.A数据和信息是两个不同的概念.B信息和数据有着密切的联系.C 2020-11-17 …