早教吧作业答案频道 -->数学-->
在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE,设∠BAC=α,∠DCE=β.(1)如图1,当点D在线段CB上,且α=60°时,那
题目详情
在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE,设∠BAC=α,∠DCE=β.
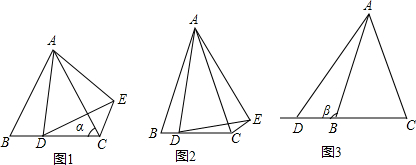
(1)如图1,当点D在线段CB上,且α=60°时,那么β=___度;
(2)当α≠60°.
①如图2,当点D在线段CB上,求α与β间的数量关系;
②如图3,当点D在线段CB的延长线上,请将如图3补充完整,并求出α与β之间的数量关系.
(1)如图1,当点D在线段CB上,且α=60°时,那么β=___度;
(2)当α≠60°.
①如图2,当点D在线段CB上,求α与β间的数量关系;
②如图3,当点D在线段CB的延长线上,请将如图3补充完整,并求出α与β之间的数量关系.

▼优质解答
答案和解析
(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE,
∴∠ACE=∠ABC=60°,
∴β=120°,
故答案为:120°;
(2)①α+β=180°,
理由:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE,
∴∠B=∠ACE,
∴∠B+∠ACB=∠ACE+∠ACB,
∴∠B+∠ACB=∠DCE=∠β,
∵α+∠B+∠ACB=180°,
∴α+β=180°,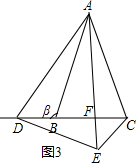
②图形正确,α=β,
∵∠DAE=∠BAC,
∴∠DAE-∠BAE=∠BAC-∠BAE,
即∠DAB=∠EAC,
在△ABD与△ACE中,
,
∴△ABD≌△ACE,
∴∠ADB=∠AEC,
设线段AE和线段CB相交于点F.
∴∠DFA=∠EFC,
∵∠DAF+∠DFA+∠ADF=∠ECF+∠EFC+∠AEC=180°,
∴∠DAF=∠ECF,
∴α=β.
∴∠BAD=∠CAE,
在△ABD与△ACE中,
|
∴△ABD≌△ACE,
∴∠ACE=∠ABC=60°,
∴β=120°,
故答案为:120°;
(2)①α+β=180°,
理由:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△ABD与△ACE中,
|
∴△ABD≌△ACE,
∴∠B=∠ACE,
∴∠B+∠ACB=∠ACE+∠ACB,
∴∠B+∠ACB=∠DCE=∠β,
∵α+∠B+∠ACB=180°,
∴α+β=180°,

②图形正确,α=β,
∵∠DAE=∠BAC,
∴∠DAE-∠BAE=∠BAC-∠BAE,
即∠DAB=∠EAC,
在△ABD与△ACE中,
|
∴△ABD≌△ACE,
∴∠ADB=∠AEC,
设线段AE和线段CB相交于点F.
∴∠DFA=∠EFC,
∵∠DAF+∠DFA+∠ADF=∠ECF+∠EFC+∠AEC=180°,
∴∠DAF=∠ECF,
∴α=β.
看了在△ABC中,AB=AC,点D...的网友还看了以下:
关于映射的题设集合A到B的映射为f1:x→y=2x+1,集合B到C的映射为f2:y→z=y²-1,则 2020-03-31 …
问科学问题,1.光从空气射入水中,当入射角变化时则()A.反射角和折射角都发生变化,B,反射角和折 2020-04-26 …
在反射弧分析实验中,捣毁青蛙的脊髓以后()A.反射、反应都消失B.反应存在、反射消失C.反射存在、 2020-05-16 …
有关反射弧的错误的表述是A.反射弧是反射的解剖学基础B.反射弧中的任何一个环节遭到破坏,反射将不能 2020-05-17 …
下列关于膝反射的叙述,错误的是()A.反射活动由一定的刺激引起B.反射活动的发生需要反射弧结构完整 2020-06-28 …
在反射弧分析实验中,捣毁青蛙的脊髓以后()A.反射、反应都消失B.反应存在、反射消失C.反射存在、 2020-06-29 …
图中P为放在匀强电场中的天然放射源,其放出的射线在电场的作用下分成a、b、c三束,以下判断正确的是 2020-07-25 …
放射性元素放出的三种射线中()A.α射线是光子流,β射线是电子流,γ射线是氦核流B.α射线是氦核流 2020-07-29 …
放射性元素放出的三种射线中()A.α射线是光子流,β射线是电子流,γ射线是氦核流B.α射线是氦核流 2020-07-29 …
光线由玻璃中射向空气时,发生完全反射的临界角是i,玻璃的折射率是多少,光在真空中速度为c,具体如下谢 2020-11-25 …