早教吧作业答案频道 -->数学-->
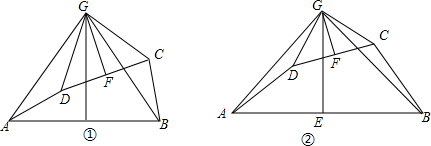
如图①②,点E、F分别是线段AB、线段CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)线段AD和线段BC有怎样的数量关系?请说明理由;
题目详情
如图①②,点E、F分别是线段AB、线段CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)线段AD和线段BC有怎样的数量关系?请说明理由;
(2)当DG⊥GC时,试判断直线AD和直线BC的位置关系,并说明理由.
(1)线段AD和线段BC有怎样的数量关系?请说明理由;
(2)当DG⊥GC时,试判断直线AD和直线BC的位置关系,并说明理由.

▼优质解答
答案和解析
(1)AD=BC.
理由:∵GF垂直平分DC,
∴GD=GC
同理,GA=GB,
在△ADG和△BCG中,
,
∴△ADG≌△BCG(SAS),
∴AD=BC;
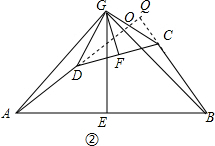 (2)AD⊥BC.
(2)AD⊥BC.
理由:延长AD,与CG相交于点O、与BC的延长线相交于点Q.
∵△ADG≌△BCG,
∴∠ADG=∠BCG,
则∠GDO=∠QCO,
∴∠QDC+∠QCD=∠DQC+∠DCG+∠QCG=∠QDC+∠GDQ+∠DCG=∠CDG+∠DCG,
∵DG⊥GC,
∴∠QDC+∠QCD=∠CDG+∠DCG=90°,
∴∠Q=90°,
∴AD⊥BC.
理由:∵GF垂直平分DC,
∴GD=GC
同理,GA=GB,
在△ADG和△BCG中,
|
∴△ADG≌△BCG(SAS),
∴AD=BC;
 (2)AD⊥BC.
(2)AD⊥BC.理由:延长AD,与CG相交于点O、与BC的延长线相交于点Q.
∵△ADG≌△BCG,
∴∠ADG=∠BCG,
则∠GDO=∠QCO,
∴∠QDC+∠QCD=∠DQC+∠DCG+∠QCG=∠QDC+∠GDQ+∠DCG=∠CDG+∠DCG,
∵DG⊥GC,
∴∠QDC+∠QCD=∠CDG+∠DCG=90°,
∴∠Q=90°,
∴AD⊥BC.
看了如图①②,点E、F分别是线段A...的网友还看了以下:
读“我国四大地理分区图”,完成3-5题.与400毫米年等降水量线北段大致吻合的是()A.A和B的分 2020-05-13 …
工业区在城市中的区位要求是①位于市中心或街道两侧②不断向市区边缘移动③不断向城市主导风向的上风向移 2020-05-15 …
工业区在城市中的区位特点是①不断向市区中心和街道两侧移动②不断向城市外围移动③不断向城市主导风向的 2020-05-15 …
如图正方形被一条曲线分成A、B两部分,下面()说法正确.A.如果a>b,那么A周长大于B周长B.如 2020-05-17 …
一个产品生产线分为A、B、C、三段,每个人每小时分别完成10、5、6、件.现在总人数为71人,要使 2020-07-17 …
公务员考试的数学题啊求助一个生产线分为a、b、c三段,每个人每小时分别完成10、5、6件,现在总人 2020-07-17 …
三角形的内角平分线定理是这样叙述的:三角形一个内角的平分线分对边所成的两条线段与这个角的两边对应成 2020-08-02 …
一个产品生产线分为a、b、c三段,每个人每小时分别完成10、5、6件,现在总人数为71人,要使得完成 2020-11-19 …
图1中A、B分别代表我国两条重要的自然地理界线,读图回答问题.(1)A线是我国1月℃等温线通过的地方 2020-12-05 …
急:指出几种常见永磁体磁场磁感线分布A条形磁体,B蹄形磁体,C两个条形磁体,左边的条形磁体右侧为N极 2020-12-22 …