早教吧作业答案频道 -->数学-->
古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似
题目详情
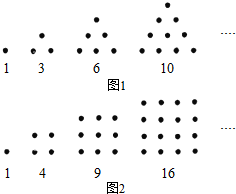
古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…,这样的数位正方形数(四边形数).
(1)请你写出既是三角形数又是正方形数且大于1的最小正整数为___;
(2)试证明:当k为正整数时,k(k+1)(k+2)(k+3)+1必须为正方形数;
(3)记第n个k变形数位N(n,k)(k≥3).例如N(1,3)=1,N(2,3)=3,N(2,4)=4.
①试直接写出N(n,3)N(n,4)的表达式;
②通过进一步的研究发现N(n,5)=
n2-
n,N(n,6)=2n2-n,…,请你推测N(n,k)(k≥3)的表达式,并由此计算N(10,24)的值.

(1)请你写出既是三角形数又是正方形数且大于1的最小正整数为___;
(2)试证明:当k为正整数时,k(k+1)(k+2)(k+3)+1必须为正方形数;
(3)记第n个k变形数位N(n,k)(k≥3).例如N(1,3)=1,N(2,3)=3,N(2,4)=4.
①试直接写出N(n,3)N(n,4)的表达式;
②通过进一步的研究发现N(n,5)=
| 3 |
| 2 |
| 1 |
| 2 |
▼优质解答
答案和解析
(1) ∵正方形数点的个数是为n2,∴除1外,分别为4,9,16,25,36,49,64,…,
∵图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即三角形数点的个数是为
,
∵4=
无正整数解,∴4不是三角形数,
∵9=
无正整数解,∴9不是三角形数,
∵16=
无正整数解,∴16不是三角形数,
∵25=
无正整数解,∴25不是三角形数,
∵36=
,解得n=8,所以36是三角形数,
∴除1外,最小的既是三角形数又是正方形数的是36,
故答案为36;
(2)证明:∵k(k+1)(k+2)(k+3)+1
=k(k+3)(k+1)(k+2)+1
=(k2+3k)(k2+3k+2)+1
=(k2+3k)2+2(k2+3k)+1
=(k2+3k+1)2
∴k(k+1)(k+2)(k+3)+1是完全平方数,即为正方形数;
(3) ①由(1)知:N(n,3)=
,N(n,4)=n2;
②∵N(n,3)=
=
=
,
N(n,4)=n2=
=
,
N(n,5)=
n2-
n=
=
,
N(n,6)=2n2-n=
=
,
∴由此变化规律可推断N(n,k)=
(k≥3);
∴N(10,24)=
=1000.
∵图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即三角形数点的个数是为
| n(n+1) |
| 2 |
∵4=
| n(n+1) |
| 2 |
∵9=
| n(n+1) |
| 2 |
∵16=
| n(n+1) |
| 2 |
∵25=
| n(n+1) |
| 2 |
∵36=
| n(n+1) |
| 2 |
∴除1外,最小的既是三角形数又是正方形数的是36,
故答案为36;
(2)证明:∵k(k+1)(k+2)(k+3)+1
=k(k+3)(k+1)(k+2)+1
=(k2+3k)(k2+3k+2)+1
=(k2+3k)2+2(k2+3k)+1
=(k2+3k+1)2
∴k(k+1)(k+2)(k+3)+1是完全平方数,即为正方形数;
(3) ①由(1)知:N(n,3)=
| n(n+1) |
| 2 |
②∵N(n,3)=
| n(n+1) |
| 2 |
| n2+n |
| 2 |
| (3-2)n2+(4-3)n |
| 2 |
N(n,4)=n2=
| 2n2+0×n |
| 2 |
| (4-2)n2+(4-4)n |
| 2 |
N(n,5)=
| 3 |
| 2 |
| 1 |
| 2 |
| 3n2-n |
| 2 |
| (5-2)n2+(4-5)n |
| 2 |
N(n,6)=2n2-n=
| 4n2-2n |
| 2 |
| (6-2)n2+(4-6)n |
| 2 |
∴由此变化规律可推断N(n,k)=
| (k-2)n2+(4-k)n |
| 2 |
∴N(10,24)=
| (24-2)×102+(4-24)×10 |
| 2 |
看了古希腊毕达哥拉斯学派的数学家常...的网友还看了以下:
数学帝书速来,将角19π分之5表示为2kπ加a(k属于z)则|a|最小角a是?……还有sin15度 2020-04-11 …
Word中如何来绘制一些数学图形?比如:数学中的三角形,绘制出高,然后把高分成的两个三角形的其中的 2020-05-16 …
据报道,英国科学家从人皮肤细胞中提取出细胞核,植入剔除了细胞核的牛卵细胞中,从而培育出人兽混合胚胎 2020-06-26 …
从物理学角度来说,下列说法中指音调的是,指响度的是(填序号)A、平常说的“引吭高歌”和�从物理学角 2020-06-28 …
从汉语词典上抄的词的解释在论文中怎么称呼?比如,抄了现代汉语词典上一个“系统”这个词的解释,然后写 2020-07-10 …
在小学认识三角形的基础上我们来继续学习三角形.三角形可用符号“△”表示.例如图1中的三角形可记作“ 2020-07-25 …
数学问题,菜鸟我又来问了(注:回答的好加分!)(1)在三角形abc中CD垂直AB于D,三角形ACD 2020-08-02 …
让你集中来学高中化学的所有知识,你认为你可以压缩到多长时间学完?要最短时间哦! 2020-11-24 …
如果有小学初中高中大学的同学聚会只能去一个,从纯属情感角度出发,多数人会去哪个?不从利益那些复杂的乱 2020-11-24 …
一道高中数学题,数学高手快来帮忙.若a,b,c∈R,且a的m次方加上b的m次方等于c的m次方,1<m 2020-12-21 …