早教吧作业答案频道 -->数学-->
四边形ABCD是正方形,对角线AC,BD相交于点O.(1)如图1,点P是正方形ABCD外一点,连接OP,以OP为一边,作正方形OPMN,且边ON与边BC相交,连接AP,BN.①依题意补全图1;②判断AP与BN的数量关
题目详情
四边形ABCD是正方形,对角线AC,BD相交于点O.
(1)如图1,点P是正方形ABCD外一点,连接OP,以OP为一边,作正方形OPMN,且边ON与边BC相交,连接AP,BN.
①依题意补全图1;
②判断AP与BN的数量关系及位置关系,写出结论并加以证明;
(2)点P在AB延长线上,且∠APO=30°,连接OP,以OP为一边,作正方形OPMN,且边ON与BC的延长线恰交于点N,连接CM,若AB=2,求CM的长(不必写出计算结果,简述求CM长的过程)
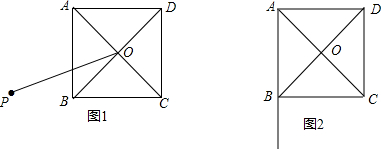
(1)如图1,点P是正方形ABCD外一点,连接OP,以OP为一边,作正方形OPMN,且边ON与边BC相交,连接AP,BN.
①依题意补全图1;
②判断AP与BN的数量关系及位置关系,写出结论并加以证明;
(2)点P在AB延长线上,且∠APO=30°,连接OP,以OP为一边,作正方形OPMN,且边ON与BC的延长线恰交于点N,连接CM,若AB=2,求CM的长(不必写出计算结果,简述求CM长的过程)

▼优质解答
答案和解析
(1)①补全图形如图1所示,
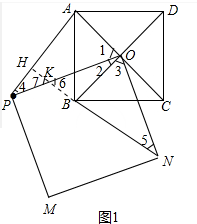
②结论:AP=BN,AP⊥BN.
理由:延长NB交AP于H,交OP于K.
∵四边形ABCD是正方形,
∴OA=OB,AO⊥BO,
∴∠1+∠2=90°,
∵四边形OPMN是正方形,
∴OP=ON,∠PON=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△APO和△BNO中,
,
∴△APO≌△BNO,
∴AP=BN,∴∠4=∠5,
在△OKN中,∠5+∠6=90°,
∵∠7=∠6,
∴∠4+∠7=90°,
∴∠PHK=90°,
∴AP⊥BN.
(2)解题思路如下:
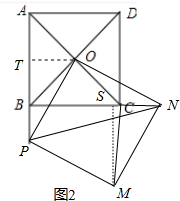
a.首先证明△APO≌△BNO,AP=BN,∠OPA=ONB.
b.作OT⊥AB于T,MS⊥BC于S,由题意可知AT=TB=1,
c.由∠APO=30°,可得PT=
,BN=AP=
+1,可得∠POT=∠MNS=60°.
d.由∠POT=∠MNS=60°,OP=MN,
可证,△OTP≌△NSM,
∴PT=MS=
,
∴CN=BN-BC=
-1,
∴SC=SN-CN=2-
,
在RT△MSC中,CM2=MS2+SC2,
∴MC的长可求.

②结论:AP=BN,AP⊥BN.
理由:延长NB交AP于H,交OP于K.
∵四边形ABCD是正方形,
∴OA=OB,AO⊥BO,
∴∠1+∠2=90°,
∵四边形OPMN是正方形,
∴OP=ON,∠PON=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△APO和△BNO中,
|
∴△APO≌△BNO,
∴AP=BN,∴∠4=∠5,
在△OKN中,∠5+∠6=90°,
∵∠7=∠6,
∴∠4+∠7=90°,
∴∠PHK=90°,
∴AP⊥BN.
(2)解题思路如下:

a.首先证明△APO≌△BNO,AP=BN,∠OPA=ONB.
b.作OT⊥AB于T,MS⊥BC于S,由题意可知AT=TB=1,
c.由∠APO=30°,可得PT=
| 3 |
| 3 |
d.由∠POT=∠MNS=60°,OP=MN,
可证,△OTP≌△NSM,
∴PT=MS=
| 3 |
∴CN=BN-BC=
| 3 |
∴SC=SN-CN=2-
| 3 |
在RT△MSC中,CM2=MS2+SC2,
∴MC的长可求.
看了四边形ABCD是正方形,对角线...的网友还看了以下:
数域p上的n维线性空间v,证明:由v的所有线性变换的线性空间L(V)是n^2维的,并找出L(V)的 2020-06-12 …
设A是数域P上的n阶方阵,令W1={X∈P^n|(A-E)X=0},W2={X∈P^n|(A+E) 2020-06-17 …
设A为属于P上的n级方阵,满足A^2-3A+2E=0,W1为(A-2E)X=0的解空间,W2为(A 2020-06-17 …
数域P上的n阶方阵是这个方阵上的数都属于P吗? 2020-06-25 …
数学统计概率问题急!离散型随机变量D(X)=np(1-p)中的n,p是什么意思,不明白,高手请你详 2020-07-15 …
读某地近地面和高空四点气压图(单位:hPa),回答29~30题.如图为“某地近地面和高空四点气压图 2020-07-20 …
证明:设A是数域P上的n阶可逆矩阵,A与对角矩阵相似的充分必要条件为A的逆矩阵与对角矩阵相似 2020-07-31 …
已知A是数域P上的n*n矩阵,设W1={AX|X∈P^n},W2={X|X∈P^n,AX=0}证明: 2020-10-31 …
选出下面各项中字音有误的一项:A泥淖nào羞赧nǎn忸怩ní泥墙nìB睥睨pìnì亲昵nì酿造nià 2020-11-07 …
读某地近地面和高空四点气压图(单位:hPa)(如图),回答3-4题.若近地面和高空四点构成热力环流, 2020-12-04 …