早教吧作业答案频道 -->数学-->
给出定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.(1)在你学过的特殊四边形中,写出两个勾股四边形的名称;(2)如图,将△ABC绕
题目详情
给出定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两个勾股四边形的名称;
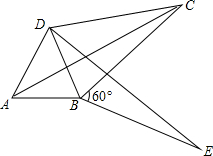
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°后得到△DBE,连接
AD、DC,若∠DCB=30°,求证:四边形ABCD是勾股四边形.

(1)在你学过的特殊四边形中,写出两个勾股四边形的名称;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°后得到△DBE,连接
AD、DC,若∠DCB=30°,求证:四边形ABCD是勾股四边形.
▼优质解答
答案和解析
(1) 直角梯形和矩形为勾股四边形;
(2)证明:连接CE,如图,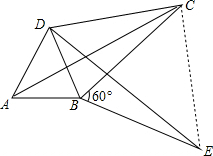
∵△ABC绕顶点B按顺时针方向旋转60°后得到△DBE,
∴BC=BE,∠CBE=60°,AC=DE,
∴△BCE为等边三角形,
∴∠BCE=60°,BC=CE,
而∠DCB=30°,
∴∠DCE=30°+60°=90°,
在Rt△DCE中,CD2+CE2=BD2,
∴CD2+CB2=AC2,
∴四边形ABCD是勾股四边形.
(2)证明:连接CE,如图,

∵△ABC绕顶点B按顺时针方向旋转60°后得到△DBE,
∴BC=BE,∠CBE=60°,AC=DE,
∴△BCE为等边三角形,
∴∠BCE=60°,BC=CE,
而∠DCB=30°,
∴∠DCE=30°+60°=90°,
在Rt△DCE中,CD2+CE2=BD2,
∴CD2+CB2=AC2,
∴四边形ABCD是勾股四边形.
看了 给出定义:若一个四边形中存在...的网友还看了以下:
由四边形各边中点组成的四边形称为“中点四边形”.如图,在四边形ABCD中,已知E、F、G、H分别是 2020-05-01 …
这几个字读什么音?左边“山”右边“由”这个字读什么音?左边山右边是恒的右半部分这个字读什么音?左边 2020-05-14 …
我们知道,顺次连接任意四边形各边中点所得四边形是平行四边形,那么顺次连接等腰梯形各边中点所得四边形 2020-05-15 …
在空格内,填上一个合适的字,使上下左右都能组合成字第一个:左边纟,右边半,上边玄,下边力,第二个: 2020-06-15 …
猜字谜:第一句:我有一物生的巧,半边鳞甲半边毛,半边离水难活命,半边入水命难保.第二句:我有一物分 2020-06-20 …
在ABC中,AB=AC,边BC的中点为D.所作的等边DEF的边EF与BC平行吗三角形ABC,AB= 2020-07-22 …
正割函数//为啥不是斜边与对边的比呢?与正炫一样在直角三角形中,任意一锐角∠A的对边与斜边的比叫做 2020-07-30 …
sinB=角B的对边比斜边和cosA=角A的邻边比斜边字母比是多少sinB=角B的对边比斜边和co 2020-07-30 …
几何三角形如已知三角形的对边A为3临边B为4时怎么算出临边与斜边的夹角度数是直角三角形A边是对边为 2020-07-30 …
1、有一个N边形的内角与外角和的比是9:2,求N边形的边数2、两个多边形边数之比是1:2内角和是3: 2020-10-31 …