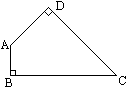
某家具加工厂的木板余料是如图所示的四边形ABCD，已知∠B＝∠D＝，∠C＝，AD＝20cm，BC＝40cm．家具厂要从这种木板余料中截出两种不同规格的矩形木板，要求截出的矩形木板的

Question

某家具加工厂的木板余料是如图所示的四边形ABCD，已知∠B＝∠D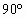＝ ，∠C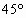＝ ，AD＝20 cm，BC＝40 cm．家具厂要从这种木板余料中截出两种不同规格的矩形木板，要求截出的矩形木板的面积尽可能地大，你能帮助家具厂设计切割方案并求出截得的矩形木板的面积吗？

Answer 1

答案：
解析：
　　按答图(1)的虚线切割可得一种规格的矩形木板(其中AE⊥AB，EF⊥BC)．因为∠C＝，∠B＝∠D＝，所以∠BAD＝．因为∠BAE＝，所以∠DAE＝，在Rt△ADE中，因为AD＝20，所以AE＝20，因为ABFE为矩形，所以BF＝AE＝20，因为BC＝40，所以CF＝40－20．所以S矩形ABFE＝AE·EF＝20×(40－20)＝800－800(cm2)． 　　按答图(2)的虚线切割可得另一种规格的矩形木板(其中AG⊥AD，GH⊥CD)．所以GH＝AD＝20．因为∠C＝，∠GHC＝，所以CG＝GH＝，所以BG＝40－，同理△ABG为等腰直角三角形，所以AG＝BG＝(40－20)＝－40．所以S矩形ABCD＝AG·GH＝(40－40)×20＝800－800(cm2)．