对于函数f(x)=(x2－2ax＋3)回答下列问题(1)若函数的定义域为R，求实数a的取值范围．(2)若函数的值域为R，求实数a的取值范围．(3)若函数在[－1，＋∞)内有意义，有实数a的

Question

对于函数f(x)=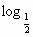 (x ² －2ax＋3)回答下列问题

(1)若函数的定义域为R，求实数a的取值范围．

(2)若函数的值域为R，求实数a的取值范围．

(3)若函数在[－1，＋∞)内有意义，有实数a的取值范围．

(4)若函数的定义域为(－∞，1)∪(3，＋∞)，求实数a的值．

(5)若函数的值域为(－∞，－1]，求实数a的值．

(6)若函数在(－∞，1]内为增函数，求实数a的取值范围．

Answer 1

答案：
解析：
　　热点分析　　这是一组概念很深刻的问题，需要熟练运用对数函数与二次函数的性质 　　热点分析　　这是一组概念很深刻的问题，需要熟练运用对数函数与二次函数的性质 　　解答　　记u＝g(x)＝x2－2ax＋3＝(x－a)2＋3－a2． 　　(1)∵u＞0对x∈R恒成立， 　　∴umin＝3－a2＞0－＜a＜， 　　∴a的取值范围是(－，)； 　　(2)这是一个较难理解的问题，从“logax的值域为R”这点思考，“u的值域为R”等价于“u＝g(x)能取遍(0，＋∞)的一切值”，或理解为“u＝g(x)的值域包含了区间(0，＋∞)”． 　　∵u＝g(x)的值域为[3－a2，＋∞)(0，＋∞)， 　　∴命题等价于umin＝3－a2≤0a≤－或a≥，∴a的取值范围是(－∞，－]∪[，＋∞)； 　　(3)应注意“在[－1，＋∞)内有意义”与定义域的概念是不同的， 　　命题等价于“u＝g(x)＞0对x∈[－1，＋∞)恒成立”，应按g(x)的对称轴x0＝a分类， 　　∴或 　　或 　　∴a的取值范围是(－2，)； 　　(4)由定义域的概念知，命题等价于 　　不等式x2－2ax＋3＞0的解集为{x|x＜1或x＞3}， 　　∴x1＝1，x2＝3是方程x2－2ax＋3＝0的两根， 　　∴a＝2，即a的值为2； 　　(5)由对数函数性质易知：g(x)的值域为[2，＋∞)，由此学生很容易得g(x)≥2，但这是不正确的，因为：“g(x)≥2”与“g(x)的值域为[2，＋∞)”并不等价，后者要求g(x)能取遍[2，＋∞)的一切值(而且不能多取)．因为g(x)的值域是[3－a2，＋∞)， 　　∴命题等于[g(x)]min＝3－a2＝2a＝±1， 　　即a的值为±1； 　　(6)命题等价于：即得a的取值范围是[1，2)． 　　评析　　学习函数知识，要非常准确地理解与掌握函数中的每个概念．许多函数的概念都有很深刻的内涵，解决问题时要仔细揣摩，才能作出准确的解答，并要在学习中不断积累经验．