早教吧作业答案频道 -->数学-->
如图(a),∠DAB+∠ABC+∠BCE=360°(1)求证:AD∥CE(2)如图(b),AG、CG分别平分∠BAD、∠BCE,BF∥AG交GC的延长线于F,判断∠ABC与∠F的数量关系,并证明;(3)如图(c),AN平分∠HAB,BP平
题目详情
如图(a),∠DAB+∠ABC+∠BCE=360°
(1)求证:AD∥CE
(2)如图(b),AG、CG分别平分∠BAD、∠BCE,BF∥AG交GC的延长线于F,判断∠ABC与∠F的数量关系,并证明;
(3)如图(c),AN平分∠HAB,BP平分∠ABC,BQ∥AN,CM平分∠BCT交BQ的反向延长线于M,①
的值不变,②
的值不变;其中只有一个结论正确,请择一证明.
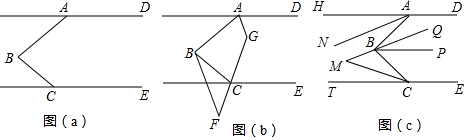
(1)求证:AD∥CE
(2)如图(b),AG、CG分别平分∠BAD、∠BCE,BF∥AG交GC的延长线于F,判断∠ABC与∠F的数量关系,并证明;
(3)如图(c),AN平分∠HAB,BP平分∠ABC,BQ∥AN,CM平分∠BCT交BQ的反向延长线于M,①
| ∠QBP |
| ∠ABC |
| ∠QMC |
| ∠ABC |

▼优质解答
答案和解析
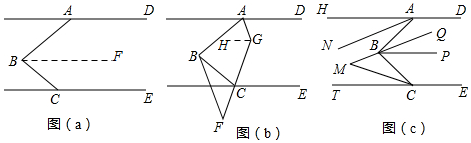 (1)过B作BF∥AD,则∠DAB+∠ABF=180°,
(1)过B作BF∥AD,则∠DAB+∠ABF=180°,
∵∠DAB+∠ABC+∠BCE=360°,
∴∠FBC+∠BCE=360°-180°=180°,
∴BF∥CE,
∴AD∥CE;
(2)∠ABC=2∠F
证明:过点G作GH∥AD,则GH∥AD∥CE,
∴∠DAG=∠AGH,∠HGC=∠GCE,
∵AG、CG分别平分∠BAD、∠BCE,
∴∠AGC=
(∠DAB+∠BCE),
∵∠DAB+∠ABC+∠BCE=360°,
∴
(∠DAB+∠ABC+∠BCE)=180°,
即∠AGC+
∠ABC=180°,
∵AG∥BF,
∴∠F+∠AGC=180°,
∴∠ABC=2∠F;
(3)②
的值不变.
证明:由上面结论可得,∠ABC=∠HAB+∠TCB,
又∵AN平分∠HAB,BP平分∠ABC,CM平分∠BCT,
∴∠ABP=∠NAB+∠MCB,
∵BQ∥AN,
∴∠NAB=∠ABQ,
∴∠QBP=
∠ABP=
∠CBP=
∠BCT=∠MCB,
∵∠QBC是△BCM的外角,
∴∠QBC=∠M+∠MCB,
∴∠M=∠QBC-∠MCB=∠QBC-∠QBP=∠PBC=
∠ABC,
即
的值为
.
 (1)过B作BF∥AD,则∠DAB+∠ABF=180°,
(1)过B作BF∥AD,则∠DAB+∠ABF=180°,∵∠DAB+∠ABC+∠BCE=360°,
∴∠FBC+∠BCE=360°-180°=180°,
∴BF∥CE,
∴AD∥CE;
(2)∠ABC=2∠F
证明:过点G作GH∥AD,则GH∥AD∥CE,
∴∠DAG=∠AGH,∠HGC=∠GCE,
∵AG、CG分别平分∠BAD、∠BCE,
∴∠AGC=
| 1 |
| 2 |
∵∠DAB+∠ABC+∠BCE=360°,
∴
| 1 |
| 2 |
即∠AGC+
| 1 |
| 2 |
∵AG∥BF,
∴∠F+∠AGC=180°,
∴∠ABC=2∠F;
(3)②
| ∠QMC |
| ∠ABC |
证明:由上面结论可得,∠ABC=∠HAB+∠TCB,
又∵AN平分∠HAB,BP平分∠ABC,CM平分∠BCT,
∴∠ABP=∠NAB+∠MCB,
∵BQ∥AN,
∴∠NAB=∠ABQ,
∴∠QBP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠QBC是△BCM的外角,
∴∠QBC=∠M+∠MCB,
∴∠M=∠QBC-∠MCB=∠QBC-∠QBP=∠PBC=
| 1 |
| 2 |
即
| ∠QMC |
| ∠ABC |
| 1 |
| 2 |
看了如图(a),∠DAB+∠ABC...的网友还看了以下:
求圆的周长,用字母表示就是C=πd或C=2πr.. 2020-04-12 …
我们怎样用”化曲为直“的方法,得出c=πd或c=2πr? 2020-04-12 …
在四边形ABCD中,若角A+角B=角C+角D,角C+2角D,则角C=答好追分! 2020-05-01 …
平行四边形ABCD中ac^2+bd^2=2ab^2类比到平行六面体ABCD-A'B'C'D'是什么 2020-05-13 …
若a>b,则下列不等式正确的是:()A.1/ab^2C.a|c|>a|c|D.a/(c^2+1)> 2020-05-20 …
如果用C表示圆的周长,那么C=兀d或C=2兀, 2020-07-13 …
证明D(cx)=c^2*D(x) 2020-07-19 …
推导圆的周长计算公式时,我们是用的方法,得出C=πd或C=2πr. 2020-07-21 …
已知A,B,C,D顺次为圆内接四边形的四个内角,求证:(1)cos((A+B)/4)=sin((C 2020-07-26 …
已知角A.B.C.D顺次为图内接四边形的四个内角,求证:sin(A/2+D)=cos(C/2-D) 2020-07-26 …