早教吧作业答案频道 -->数学-->
如图,已知正方形ABCD,E是CB延长线上一点,连接DE,交AB于点F,过点B作BG⊥DE于点G,连接AG.(1)依题意补全图形;(2)求证:∠ABG=∠ADE;(3)写出DG,AG,BG之间的等量关系,并证明.
题目详情
如图,已知正方形ABCD,E是CB延长线上一点,连接DE,交AB于点F,过点B作BG⊥DE于点G,连接AG.
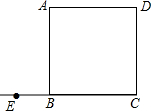
(1)依题意补全图形;
(2)求证:∠ABG=∠ADE;
(3)写出DG,AG,BG之间的等量关系,并证明.

(1)依题意补全图形;
(2)求证:∠ABG=∠ADE;
(3)写出DG,AG,BG之间的等量关系,并证明.
▼优质解答
答案和解析
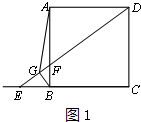 (1)补全图形,如图1;
(1)补全图形,如图1;
(2)证明∵正方形ABCD,
∴AD∥BC,
∴∠DEC=∠ADE,
∵∠ABC=90°,
∴∠FBE=90°,
∴∠ABG+∠EBG=90°,
∵BG⊥DE于点G,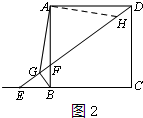
∴∠DEC+∠EBG=90°,
∴∠ABG=∠DEC,
∴∠ABG=∠ADE;
(3)DG=
AG+BG,理由是:
如图2,在DE上截取DH=BG,连接AH,
∵四边形ABCD是正方形,
∴∠DAB=90°,AB=AD,
∵∠ABG=∠ADH(已证),
∴△ABG≌△ADH(SAS),
∴AG=AH,∠GAB=∠HAD,
∴∠GAH=90°,
∴AG2+AH2=GH2,
∴GH=
AG,
∴DG=DH+GH=
AG+BG.
 (1)补全图形,如图1;
(1)补全图形,如图1;(2)证明∵正方形ABCD,
∴AD∥BC,
∴∠DEC=∠ADE,
∵∠ABC=90°,
∴∠FBE=90°,
∴∠ABG+∠EBG=90°,
∵BG⊥DE于点G,

∴∠DEC+∠EBG=90°,
∴∠ABG=∠DEC,
∴∠ABG=∠ADE;
(3)DG=
| 2 |
如图2,在DE上截取DH=BG,连接AH,
∵四边形ABCD是正方形,
∴∠DAB=90°,AB=AD,
∵∠ABG=∠ADH(已证),
∴△ABG≌△ADH(SAS),
∴AG=AH,∠GAB=∠HAD,
∴∠GAH=90°,
∴AG2+AH2=GH2,
∴GH=
| 2 |
∴DG=DH+GH=
| 2 |
看了如图,已知正方形ABCD,E是...的网友还看了以下:
求几个英文答案关于《穷爸爸和富爸爸》这本书如题,小组讨论基本问题,求一些看过此书英文水平又高的人能 2020-05-13 …
紧急一数学题求一小半圆的面积求一半圆的面积高是9直径是40是一个锅型它的面积怎么求N种答案给个准确 2020-05-16 …
急求初三动点题求一道初三动点题,要求有图,有答案,给网止也行. 2020-05-20 …
微积分的问题求一个定积分的值是怎么求的?(用牛顿尼...公式,)根本问题是不知道知道一个不定积分, 2020-07-16 …
常数项级数求和的问题求一个常数项级数的和的问题,通常对于比较复杂的级数可以先构造一个幂级数∑An* 2020-07-29 …
物资调运问题求一篇论文啊,物资调运问题某城区有29个物资需求点,需求点的地理坐标和每天物资的需求量见 2020-11-05 …
方程基本概念问题,求一个明确的解释……在一个题目中,如果有两个问题,而且要分开解,那么这两个不相干的 2020-11-16 …
求一数学难题求一数学题,能难倒我的,计算量大的无意义,高等数学往上走的没想法,历史上证不出的还是留着 2020-11-28 …
求一G开头Y结尾的4个英文的人名,急呀呀呀呀呀. 2021-02-05 …
高中力学问题将一G=10N的物体以力F按在墙上,动摩擦因素=0.2;物体匀速运动力F为多少?物体静止 2021-02-05 …