早教吧作业答案频道 -->数学-->
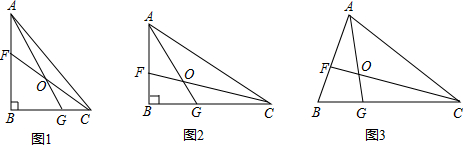
已知△ABC中,F,G分别为AB,BC上一点,AG,CF交于点O,记△ABG的面积为S1,△BFC的面积为S2,且S1=S2.(1)如图1.若∠B=90°,AB=Bc,AFBF=23,求OFOC的值;(2)如图2,若∠B=90°,AF=6,CG=8,OA=3OG
题目详情
已知△ABC中,F,G分别为AB,BC上一点,AG,CF交于点O,记△ABG的面积为S1,△BFC的面积为S2,且S1=S2.
(1)如图1.若∠B=90°,AB=Bc,
=
,求
的值;
(2)如图2,若∠B=90°,AF=6,CG=8,OA=3OG,求AC的长;
(3)如图3,若∠OAC=45°,∠OCA=30°,求证:OF=
OG.
(1)如图1.若∠B=90°,AB=Bc,
| AF |
| BF |
| 2 |
| 3 |
| OF |
| OC |
(2)如图2,若∠B=90°,AF=6,CG=8,OA=3OG,求AC的长;
(3)如图3,若∠OAC=45°,∠OCA=30°,求证:OF=
| 2 |

▼优质解答
答案和解析
(1)∵S1=S2,
∴S△ACF=S△ACG,
过F作FM⊥AC于M,GN⊥AC于N,连接FG,
∴FM=GN,
∴FG∥AC,
∴△BFG∽△BAC,
∴
=
,
∵
=
,
∴
=
=
,
∵FG∥AC,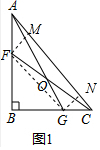
∴△FOG∽△AOC,
∴
=
=
;
(2)如图2,∵S1=S2,
∴S△ACF=S△ACG,
∴
AF•BC=
CG•AB,
∴
=
,
设AB=3k,BC=4k,
∴AC=5k,
过F作FM⊥AC于M,GN⊥AC于N,连接FG,
∴FM=GN,
∴FG∥AC,
∴△BFG∽△BAC,
∴
=
=
,
∴FG=
k,
∵BF2+BG2=FG2,
∵BF=3k-6,BG=4k-8,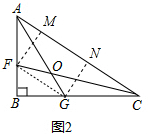
∴(3k-6)2+(4k-8)2=(
k)2,
∴k=3,k=6(不合题意),
∴AC=15;
(3)如图3,∵S1=S2,
∴S△ACF=S△ACG,
过F作FM⊥AC于M,GN⊥AC于N,连接FG,
∴FM=GN,
∴FG∥AC,
∵∠OAC=45°,∠OCA=30°,
∴∠FGA=45°,∠GFO=30°,
过O作OH⊥FG于H,
∴OH=
OG,
∵∠GFO=30°,
∴OF=2OH=
OG.
∴S△ACF=S△ACG,
过F作FM⊥AC于M,GN⊥AC于N,连接FG,
∴FM=GN,
∴FG∥AC,
∴△BFG∽△BAC,
∴
| FG |
| AC |
| BF |
| AF |
∵
| AF |
| BF |
| 2 |
| 3 |
∴
| BF |
| BA |
| FG |
| AC |
| 3 |
| 5 |
∵FG∥AC,

∴△FOG∽△AOC,
∴
| FO |
| OC |
| FG |
| AC |
| 3 |
| 5 |
(2)如图2,∵S1=S2,
∴S△ACF=S△ACG,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AB |
| BC |
| 3 |
| 4 |
设AB=3k,BC=4k,
∴AC=5k,
过F作FM⊥AC于M,GN⊥AC于N,连接FG,
∴FM=GN,
∴FG∥AC,
∴△BFG∽△BAC,
∴
| FG |
| AC |
| OG |
| AO |
| 1 |
| 3 |
∴FG=
| 5 |
| 3 |
∵BF2+BG2=FG2,
∵BF=3k-6,BG=4k-8,

∴(3k-6)2+(4k-8)2=(
| 5 |
| 3 |
∴k=3,k=6(不合题意),
∴AC=15;
(3)如图3,∵S1=S2,
∴S△ACF=S△ACG,
过F作FM⊥AC于M,GN⊥AC于N,连接FG,
∴FM=GN,

∴FG∥AC,
∵∠OAC=45°,∠OCA=30°,
∴∠FGA=45°,∠GFO=30°,
过O作OH⊥FG于H,
∴OH=
| ||
| 2 |
∵∠GFO=30°,
∴OF=2OH=
| 2 |
看了已知△ABC中,F,G分别为A...的网友还看了以下:
已知a,b,c均为整数,且a-b的绝对值的三次方+c-a的绝对值的平方=1,求a-c的绝对值+c- 2020-04-05 …
已知a,b,c均为整数,且a-b的绝对值的三次方+c-a的绝对值的平方=1,求a-c的绝对值+c- 2020-06-24 …
2003年春季前后是服装、鞋帽畅销时期,各大商场抓住这商机,采取打折让利的促销手段。商家打折让利促 2020-06-26 …
14.表达式是满足:当c的值为1、3、5三个数中任意一个时值为“真”,否则值为“假”的表达式A)( 2020-07-13 …
甲表有A、B二列,同列内为不重复数值;乙表有C、D二列,C列为不规则重复的数值,B列空白.求:如果 2020-07-23 …
已知函数f(x)是R上的单调增函数且为奇函数,f(1)的值?A恒为正值B恒为负值C恒为0D可正可负 2020-08-01 …
执行如图所示的程序框图,正确的是()A.若输入a,b,c的值依次为1,2,3,则输出的值为5B.若输 2020-12-15 …
如图:D,E分别是△ABC的边BC、AC上的点,若AB=AC,AD=AE,则()A.当∠B为定值时, 2020-12-31 …
如图:D,E分别是△ABC的边BC、AC上的点,若AB=AC,AD=AE,则()A.当∠B为定值时, 2020-12-31 …
第一题:如果两个数的积为负数,和为正数,则两个数()A均为正数B一正一负,且负数的绝对值大于正数的绝 2021-01-22 …