早教吧作业答案频道 -->数学-->
问题再现:如图1:△ABC中,AF为BC边上的中线,则S△ABF=S△ACP=12S△ABC由这个结论解答下列问题:问题解决:问题1:如图2,△ABC中,CD为AB边上的中线,BE为AC边上的中线,
题目详情
问题再现:
如图1:△ABC中,AF为BC边上的中线,则S△ABF=S△ACP=
S△ABC
由这个结论解答下列问题:
问题解决:
问题1:如图2,△ABC中,CD为AB边上的中线,BE为AC边上的中线,则S△BOC=S四边形ADOE.
分析:△ABC中,CD为AB边上的中线,则S△BCD=
S△ABC,BE为AC边上的中线,则S△ABE=
S△ABC
∴S△BCD=S△ABE
∴S△BCD-S△BOD=S△ABE-S△BOD
又∵S△BOC=S△BCD-S△BOD,S四边形ADOE=S△ABE-S△BOD
即S△BOC=S四边形ADOE
问题2:如图3,△ABC中,CD为AB边上的中线,BE为AC边上的中线,AF为BC边上的中线.
(1)S△BOD=S△COE吗?请说明理由.
(2)请直接写出△BOD的面积与△ABC的面积之间的数量关系:S△BOD=___S△ABC.
问题拓广:
(1)如图4,E、F分别为四边形ABCD的边AD、BC的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴=___S四边形ABCD.
(2)如图5,E、F、G、H分别为四边形ABCD的边AD、BC、AB、CD的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴=___S四边形ABCD.
(3)如图6,E、F、G、H分别为四边形ABCD的边AD、BC、AB、CD的中点,
若S△AME=1、S△BNG=1.5、S△CQF=2、S△BFH△DFH=2.5,则S阴=___.
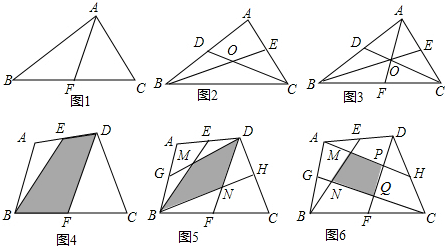
如图1:△ABC中,AF为BC边上的中线,则S△ABF=S△ACP=
| 1 |
| 2 |
由这个结论解答下列问题:
问题解决:
问题1:如图2,△ABC中,CD为AB边上的中线,BE为AC边上的中线,则S△BOC=S四边形ADOE.
分析:△ABC中,CD为AB边上的中线,则S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BCD=S△ABE
∴S△BCD-S△BOD=S△ABE-S△BOD
又∵S△BOC=S△BCD-S△BOD,S四边形ADOE=S△ABE-S△BOD
即S△BOC=S四边形ADOE
问题2:如图3,△ABC中,CD为AB边上的中线,BE为AC边上的中线,AF为BC边上的中线.
(1)S△BOD=S△COE吗?请说明理由.
(2)请直接写出△BOD的面积与△ABC的面积之间的数量关系:S△BOD=___S△ABC.
问题拓广:
(1)如图4,E、F分别为四边形ABCD的边AD、BC的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴=___S四边形ABCD.
(2)如图5,E、F、G、H分别为四边形ABCD的边AD、BC、AB、CD的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴=___S四边形ABCD.
(3)如图6,E、F、G、H分别为四边形ABCD的边AD、BC、AB、CD的中点,
若S△AME=1、S△BNG=1.5、S△CQF=2、S△BFH△DFH=2.5,则S阴=___.

▼优质解答
答案和解析
问题2::S△BOD=S△COE成立,
理由:∵△ABC中,CD为AB边上的中线,
∴S△BCD=
S△ABC,
∵BE为AC边上的中线,
∴S△CBE=
S△ABC
∴S△BCD=S△CBE
∵S△BCD=S△BOD+S△BOC,S△CBE=S△COE+S△BOC
∴S△BOD=S△COE
(2)由(1)有S△BOD=S△COE,
同(1)方法得,S△BOD=S△AOD,
S△COE=S△AOE,
S△BOF=S△COF,
∴S△BOD=S△COE=S△AOE=S△AOD,
∵点O是三角形三条中线的交点,
∴OA=2OF,
∴S△AOC=2S△COF=S△AOE+S△COE=2S△COE,
∴S△COF=S△COE,
∴S△BOD=S△COE=S△AOE=S△AOD=S△BOF=S△COF,
∴S△BOD=
S△ABC,
故答案为
问题拓广:
(1)如图4:
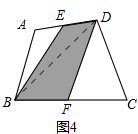
连接BD,由问题再现:
S△BDE=
S△ABD,
S△BDF=
S△BCD,
∴S阴影=
S四边形ABCD,
故答案为
,
(2)如图5:
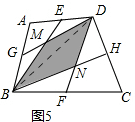
连接BD,由问题解决:
S△BMD=
S△ABD,S△BDN=
S△BCD,
∴S阴影=
S四边形ABCD,
故答案为
;
(3)如图6,
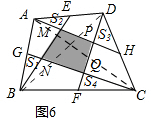
连接AC,BD
由上面的结论得
∵G是四边形ABCD的边AB的中点,
∴S△AGC=
S△ABC,S△BGC=
S△ABC
∵H是四边形ABCD的边CD的中点
∴S△AHC=
S△ACD,S△AHD=
S△ACD
∴S四边形AGCH=
S四边形ABCD
同样的方法得到S四边形BFDE=
S四边形ABCD
∴S四边形AGCH=S四边形BFDE
∴S四边形AGCH=S△ABE+S△DFC
∴S阴=S1+S2+S3+S4=1+1.5+2+2.5=7.
故答案为7.
理由:∵△ABC中,CD为AB边上的中线,
∴S△BCD=
| 1 |
| 2 |
∵BE为AC边上的中线,
∴S△CBE=
| 1 |
| 2 |
∴S△BCD=S△CBE
∵S△BCD=S△BOD+S△BOC,S△CBE=S△COE+S△BOC
∴S△BOD=S△COE
(2)由(1)有S△BOD=S△COE,
同(1)方法得,S△BOD=S△AOD,
S△COE=S△AOE,
S△BOF=S△COF,
∴S△BOD=S△COE=S△AOE=S△AOD,
∵点O是三角形三条中线的交点,
∴OA=2OF,
∴S△AOC=2S△COF=S△AOE+S△COE=2S△COE,
∴S△COF=S△COE,
∴S△BOD=S△COE=S△AOE=S△AOD=S△BOF=S△COF,
∴S△BOD=
| 1 |
| 6 |
故答案为
| 1 |
| 6 |
问题拓广:
(1)如图4:

连接BD,由问题再现:
S△BDE=
| 1 |
| 2 |
S△BDF=
| 1 |
| 2 |
∴S阴影=
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
(2)如图5:

连接BD,由问题解决:
S△BMD=
| 1 |
| 3 |
| 1 |
| 3 |
∴S阴影=
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
(3)如图6,

连接AC,BD
由上面的结论得
∵G是四边形ABCD的边AB的中点,
∴S△AGC=
| 1 |
| 2 |
| 1 |
| 2 |
∵H是四边形ABCD的边CD的中点
∴S△AHC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形AGCH=
| 1 |
| 2 |
同样的方法得到S四边形BFDE=
| 1 |
| 2 |
∴S四边形AGCH=S四边形BFDE
∴S四边形AGCH=S△ABE+S△DFC
∴S阴=S1+S2+S3+S4=1+1.5+2+2.5=7.
故答案为7.
看了问题再现:如图1:△ABC中,...的网友还看了以下:
两辆汽车a、b在同一平道公路上运动的x-t和v-t图象分别如图甲和图乙所示,由图象可知()A.甲、 2020-04-06 …
分析如图,图1中A、B、C、D表示液体,a、b、c、d表示结构,请回答问题:(1)据图1写出以下各 2020-04-06 …
假设数组A[n]的n个元素中有多个零元素,设计一个算法,将A中所有的非零元素依次移到A的前端1算法 2020-04-26 …
(1)(a)图1中小朋友用力推车,虽然累得满头大汗,可是车却一动不动.(a)图1中,小孩是劳而无“ 2020-05-13 …
读图A“中国年降水量分布图”和图B“中国农业的地区分布图”,回答下列问题(1)在图A中找到800毫 2020-05-13 …
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系 2020-05-16 …
如图中A图表示某些生态系统的能量锥体图,P为生产者,Q1为初级消费者,Q2为次级消费者.B图是将A 2020-06-13 …
直角坐标系中,一个图案上各个点的横坐标和纵坐标分别加正数a(a>1),那么所得的图案与原来图案相比 2020-06-21 …
如图为医院为病人输液的部分装置,图中A未输液瓶,B为滴壶,C为进气管.与大气相通.则在输液过程中( 2020-07-12 …
图为医院为病人输液的部分装置,图中A为输液瓶,B为滴壶,C为进气管,与大气相通.则在输液过程中(瓶 2020-07-16 …