如图，在△ABC中，AB=AC=10，BC=16，点D是边BC上（不与B，C重合）一动点，∠ADE=∠B=α，DE交AC于点E．下列结论：①AD2=AE•AB；②3.6≤AE<10；③当AD=210时，△ABD≌△DCE；④△DCE为直角三角形时，BD

Question

如图，在△ABC中，AB=AC=10，BC=16，点D是边BC上（不与B，C重合）一动点，∠ADE=∠B=α，DE交AC于点E．下列结论：
①AD²=AE•AB；
②3.6≤AE<10；
③当AD=2

√(10)时，△ABD≌△DCE；
④△DCE为直角三角形时，BD为8或12.5．
其中正确的结论个数是（　　）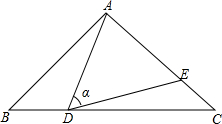

A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

①∵AB=AC，
∴∠B=∠C，
又∵∠ADE=∠B
∴∠ADE=∠C，
∴△ADE∽△ACD，
∴(AD)/(AE)=(AB)/(AD)
∴AD²=AE•AB，
故①正确，
②易证得△CDE∽△BAD，∵BC=16，
设BD=y，CE=x，
∴(AB)/(CD)=(BD)/(CE)，
∴(10)/(16-y)=(y)/(x)，
整理得：y²-16y+64=64-10x，
即（y-8）²=64-10x，
∴0<x≤6.4，
∵AE=AC-CE=10-x，
∴3.6≤AE<10．
故②正确．
③作AG⊥BC于G，
∵AB=AC=10，∠ADE=∠B=α，cosα=(4)/(5)，
∵BC=16，
∴CG=(1)/(2)BC=8，
∴AG=6，
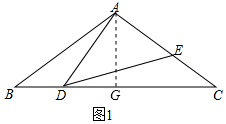（1）当点D在G点左侧时，如图1所示，
∵AD=2√(10)，
∴DG=2，
∴CD=CG+DG=8+2=10，
∴AB=CD，
∴△ABD与△DCE全等；
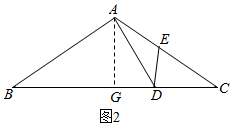（2）当点D在G点右侧时，如图2所示，
∵AD=2√(10)，
∴DG=2，
∴CD=CG-DG=8-2=6，
∴AB≠CD，
∴△ABD与△DCE不全等；
故③错误；
④当∠AED=90°时，由①可知：△ADE∽△ACD，
∴∠ADC=∠AED，
∵∠AED=90°，
∴∠ADC=90°，
即AD⊥BC，
∵AB=AC，
∴BD=CD，
∴∠ADE=∠B=α且cosα=(4)/(5)，AB=10，
BD=8．
当∠CDE=90°时，易△CDE∽△BAD，
∵∠CDE=90°，
∴∠BAD=90°，
∵∠B=α且cosα=(4)/(5)．AB=10，
∴cosB=(AB)/(BD)=(4)/(5)，
∴BD=12.5．
故④正确．
故选C．