早教吧作业答案频道 -->数学-->
如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(Ⅰ)证明:CE∥平面PAB;(Ⅱ)求直线CE与平面PBC所成角的正弦值.
题目详情
如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
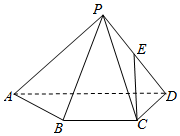
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.

(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
▼优质解答
答案和解析
证明:(Ⅰ)取AD的中点F,连结EF,CF,∵E为PD的中点,∴EF∥PA,在四边形ABCD中,BC∥AD,AD=2DC=2CB,F为中点,∴CF∥AB,∴平面EFC∥平面ABP,∵EC⊂平面EFC,∴EC∥平面PAB. (Ⅱ)连结BF,过F作FM⊥PB于M,连...
看了如图,已知四棱锥P-ABCD,...的网友还看了以下:
已知弧长弦长求半径弧长830弦长800我是用公式2ar=830sina=(L/2)/r设a为扇形圆 2020-05-13 …
下列符合公文用语要求的是( )A.为了形象,可使用口语、歇后语等B.为了使文章贴近大众,可使用方 2020-05-31 …
A为p*q矩阵,B为q*p矩阵,证明det(E+AB)=det(E+BA) 2020-06-03 …
假设A为B的子集合,证明P(A)为P(B)的子集合很急的作业``谁能帮我证明一下```请详细些`谢 2020-06-14 …
用一张锐角三角形纸片ADC折出一个菱形,使∠A为菱形的一个内角,并说明理由. 2020-06-15 …
尺规作图:(不写作法,保留作图痕迹)已知:锐角△ABC,求作:菱形AMPN,使得∠A为菱形APMN 2020-06-30 …
(2011•郑州模拟)在三角形ABC中,∠C=90°,AC=BC=10厘米,A为扇形AEF的圆心, 2020-07-26 …
设集合,的子集,其中,当满足时,我们称子集A为P的“好子集”,则这种“好子集”的个数为.(用数字作 2020-07-29 …
如图所示,光滑的弧形槽的半径为R(R>>MN弧),A为弧形槽的最低点,小球B放在A点正上方离A点正上 2020-12-25 …
a+b>=2根号ab,p反比例上任一点,过p做x,y轴的垂线交点为C,D.A(四边形面积最小时,四边 2020-12-25 …