早教吧作业答案频道 -->数学-->
如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.(1)求∠CDO的度数;(2)
题目详情
如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.
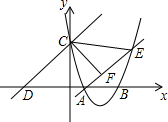
(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD-S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.

(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD-S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.
▼优质解答
答案和解析
(1)∵直线l:y=x+2t与y轴点C,交x轴于点D,
∴C(0,2t),D(-2t,0)
∴OC=OD,
∵∠COD=90°,
∴∠CDO=∠DCO=45°.
(2)如图1,作FG⊥x轴于点G,FH⊥y轴于点H,
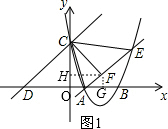
∵∠HOG=∠OGF=∠FHO=90°,
∴四边形OGFH是矩形
∴∠HFG=90°,
∴∠HFA+∠AFG=90°
又∵CF⊥AE,
∴∠CFH+∠HFA=90°
∴∠CFH=∠AFG,
又∵∠CAE=∠CDO=45°,
∴∠FCA=45°,
∴CF=AF,
又∵∠FGA=∠CHF=90°,
在△FGA和△FHC中,
∴△FGA≌△FHC,
∴FH=FG,HC=AG,
设F(m,m)
则2t-m=m-2,
得m=t+1,
∴F(t+1,t+1).
(3)∵S△COD-S四边形COAF=S△COD-S正方形HOGF=7
∴
(2t)2-(t+1)2=7,
解得:t=4或-2(舍去),
则A点坐标(2,0),B点坐标(4,0),C点坐标(0,8)
设y=a(x-2)(x-4),
把C(0,8)代入y=a(x-2)(x-4),
解得a=1,
∴y=(x-2)(x-4)=x2-6x+8.
(4)t=3或2.
如图2,作ET⊥HF于T,
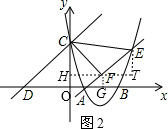
求得:E的横坐标是
,CH=t-1,FT=
,
由△HCF∽△TFE,
则
=
,
得:
=
当△OBC∽△FEC时,
=
=2,
即
=2,
解得:t=3或t=-1( 舍去),
当△OBC∽△FCE时,
=
=
,
即
=
,
解得:t=2或t=0(舍去).
∴t=3或2.
∴C(0,2t),D(-2t,0)
∴OC=OD,
∵∠COD=90°,
∴∠CDO=∠DCO=45°.
(2)如图1,作FG⊥x轴于点G,FH⊥y轴于点H,

∵∠HOG=∠OGF=∠FHO=90°,
∴四边形OGFH是矩形
∴∠HFG=90°,
∴∠HFA+∠AFG=90°
又∵CF⊥AE,
∴∠CFH+∠HFA=90°
∴∠CFH=∠AFG,
又∵∠CAE=∠CDO=45°,
∴∠FCA=45°,
∴CF=AF,
又∵∠FGA=∠CHF=90°,
在△FGA和△FHC中,
|
∴△FGA≌△FHC,
∴FH=FG,HC=AG,
设F(m,m)
则2t-m=m-2,
得m=t+1,
∴F(t+1,t+1).
(3)∵S△COD-S四边形COAF=S△COD-S正方形HOGF=7
∴
| 1 |
| 2 |
解得:t=4或-2(舍去),
则A点坐标(2,0),B点坐标(4,0),C点坐标(0,8)
设y=a(x-2)(x-4),
把C(0,8)代入y=a(x-2)(x-4),
解得a=1,
∴y=(x-2)(x-4)=x2-6x+8.
(4)t=3或2.
如图2,作ET⊥HF于T,

求得:E的横坐标是
| t2+1 |
| t-1 |
| 2 |
| t-1 |
由△HCF∽△TFE,
则
| CH |
| FT |
| CF |
| EF |
得:
| (t-1)2 |
| 2 |
| CF |
| EF |
当△OBC∽△FEC时,
| OC |
| OB |
| CF |
| EF |
即
| (t-1)2 |
| 2 |
解得:t=3或t=-1( 舍去),
当△OBC∽△FCE时,
| OB |
| OC |
| CF |
| EF |
| 1 |
| 2 |
即
| (t-1)2 |
| 2 |
| 1 |
| 2 |
解得:t=2或t=0(舍去).
∴t=3或2.
看了如图,已知抛物线经过点A(2,...的网友还看了以下:
离心率是e的曲线怎么设?求高手!一个圆锥曲线,书上直接设了(1-e^2)x^2+y^2-2e^2p 2020-04-13 …
ab=c^2怎么推出√(e^2-1)=e^2..(双曲线,e是离心率)RT我省略了系数,没想到出B 2020-05-15 …
选用所给的句子完成下列对话,将句子抄写在相应的横线上.E:Hobo,todayisHallowee 2020-05-16 …
求∫(0到1)(1/e)xdx+∫(0到1)[(1/e)x-lnx]dx我算出前面的∫(0到1)( 2020-05-20 …
己知抛物线与x轴交于A-1,0B3,0两点,与y轴交于0,1.E是线段BC上一个动点(与点B,C不 2020-06-19 …
设函数f(x)=alnx-bx^2(x>0)(1)若函数f(x)在x=1处与直线y=-1/2相切, 2020-07-31 …
已知函数f(x)=alnx+bex(a,b为常数,无理数e=2.71828…是自然对数的底数),曲 2020-08-01 …
(1)计算对数函数y=lnx对应于x取1/e^2,1/e,1,e,e^2时的函数值(2)计算对数函 2020-08-02 …
EXCEL计算k3=1/1+e(2+2.23c3+3d3+2.4e3)这个怎么算k3=1/1+e(2 2020-10-31 …
用C++求不超过30000E数列的最大E数的值/*数列:E(1)=E(2)=1E(n)=(n-1)* 2020-11-20 …