早教吧作业答案频道 -->数学-->
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.(1)求证:三角形DEB是等腰三角形;(2)判断AF与BD是否平行,并说明理由.
题目详情
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
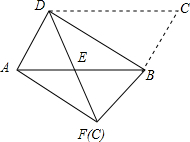
(1)求证:三角形DEB是等腰三角形;
(2)判断AF与BD是否平行,并说明理由.

(1)求证:三角形DEB是等腰三角形;
(2)判断AF与BD是否平行,并说明理由.
▼优质解答
答案和解析
(1)由折叠可知:∠CDB=∠EDB,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=∠EBD,
∴∠EDB=∠EBD,
∴△BDE是等边三角形;
(2)AF∥DB;
∵∠EDB=∠EBD,
∴DE=BE,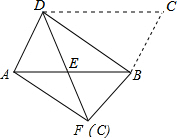
由折叠可知:DC=DF,
∵四边形ABCD是平行四边形,
∴DC=AB,
∴DF=AB,
∴AE=EF,
∴∠EAF=∠EFA,
在△BED中,∠EDB+∠EBD+∠DEB=180°,
∴2∠EDB+∠DEB=180°,
同理,在△AEF中,2∠EFA+∠AEF=180°,
∵∠DEB=∠AEF,
∴∠EDB=∠EFA,
∴AF∥DB.
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=∠EBD,
∴∠EDB=∠EBD,
∴△BDE是等边三角形;
(2)AF∥DB;
∵∠EDB=∠EBD,
∴DE=BE,

由折叠可知:DC=DF,
∵四边形ABCD是平行四边形,
∴DC=AB,
∴DF=AB,
∴AE=EF,
∴∠EAF=∠EFA,
在△BED中,∠EDB+∠EBD+∠DEB=180°,
∴2∠EDB+∠DEB=180°,
同理,在△AEF中,2∠EFA+∠AEF=180°,
∵∠DEB=∠AEF,
∴∠EDB=∠EFA,
∴AF∥DB.
看了如图,将平行四边形ABCD沿对...的网友还看了以下:
骑车从点a沿正东方向到点b后行驶方向改为北偏西70°,到达c处后偏离行驶方向70°向d前进,现行驶方 2020-03-31 …
三个整数p,q,r满足条件0小于p小于q小于r,它们分别写在三张卡片上,a,b,c三人进行某种游戏 2020-05-13 …
三个整数p、q、r满足条件0<p<q<r,它们分别写在三张卡片上,A、B、C三人进行某种游戏,每次 2020-06-12 …
甲、乙、丙三人同时从A出发去B,甲、乙到B后调头回A,并且调头后速度减少到各自原来速度的一半.甲最 2020-06-13 …
三思后行记心中2013年10月以来,细心的市民或许会发现,淮安街头上多了一道亮丽的风景:崭新的公共 2020-06-26 …
要做到对自己的行为负责,我们应该()A.在行动前仔细考虑,做出最优化选择B.对行为后果的自省及自觉 2020-06-27 …
三思后行记心中2013年10月以来,细心的市民或许会发现,淮安街头上多了一道亮丽的风景:崭新的公共 2020-06-27 …
两辆汽车分别从A,B两地同时相对而行,三小时后甲车行驶了全程的八分之三,乙车行驶了全程的四分之三看 2020-07-18 …
1、甲、乙、丙三人都要从A地到B地去,但只有两辆自行车,而自行车又不许带人,但可以放在中途某处,后 2020-07-20 …
人的活动具有“先思而后行”的特点,即所谓“三思而行”.这表明哲学人的活动具有“先思而后行”的特点,即 2020-11-29 …