如图，AB为O的直径，点C为圆外一点，连接AC、BC，分别与O相交于点D、点E，且AD=DE，过点D作DF⊥BC于点F，连接BD、DE、AE．（1）求证：DF是O的切线；（2）试判断△DEC的形状，并说明理由；（

Question

如图，AB为 O的直径，点C为圆外一点，连接AC、BC，分别与 O相交于点D、点E，且

AD

=

DE

，过点D作DF⊥BC于点F，连接BD、DE、AE．

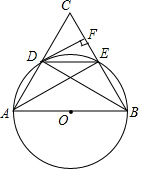
（1）求证：DF是 O的切线；
（2）试判断△DEC的形状，并说明理由；
（3）若 O的半径为5，AC=12，求sin∠EAB的值．

Answer 1

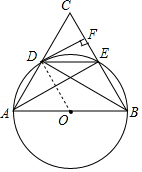证明：（1）连接OD，
∵

AD

=

DE

，
∴∠ABD=∠DBC，
∵AB是 O的直径，
∴∠ADB=∠CDB=90°，
∵BD=BD，
∴△ABD≌△CBD，
∴AD=CD，
∵OA=OB，
∴OD是△ABC的中位线，
∴OD∥BC，
∵DF⊥BC，
∴DF⊥OD，
∴DF是 O的切线；
（2）△DEC是等腰三角形，理由是：
∵

AD

=

DE

，
∴AD=DE，
∵AD=CD，
∴CD=DE，
∴△DEC是等腰三角形；
（3）∵ O的半径为5，
∴BC=AB=10，
∵AB是 O的直径，
∴∠AEB=90°，
设BE=x，则CE=10-x，
由勾股定理得：12²-（10-x）²=10²-x²，
解得：x=(14)/(5)，
∴BE=(14)/(5)，
在Rt△AEB中，sin∠EAB=(BE)/(AB)=((14)/(5))/(10)=(7)/(25)．