早教吧作业答案频道 -->数学-->
在Rt△ABC中,∠B=90°,AB=BC=12cm,点D从点A出发沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上).设点D移动的时间为t秒.试解答下列问题:(1)如图1
题目详情
在Rt△ABC中,∠B=90°,AB=BC=12cm,点D从点A出发沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上).设点D移动的时间为t秒.
试解答下列问题:
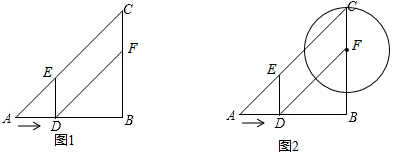
(1)如图1,当t为多少秒时,四边形DFCE的面积等于20cm2?
(2)如图1,点D在运动过程中,四边形DFCE可能是菱形吗?若能,试求t的值;若不能,请说明理由;
(3)如图2,以点F为圆心,FC的长为半径作 F.
①在运动过程中,是否存在这样的t值,使 F正好与四边形DFCE的一边(或边所在的直线)相切?若存在,求出t值;若不存在,请说明理由;
②若 F与四边形DFCE至多有两个公共点,请直接写出t的取值范围.
试解答下列问题:
(1)如图1,当t为多少秒时,四边形DFCE的面积等于20cm2?
(2)如图1,点D在运动过程中,四边形DFCE可能是菱形吗?若能,试求t的值;若不能,请说明理由;
(3)如图2,以点F为圆心,FC的长为半径作 F.
①在运动过程中,是否存在这样的t值,使 F正好与四边形DFCE的一边(或边所在的直线)相切?若存在,求出t值;若不存在,请说明理由;
②若 F与四边形DFCE至多有两个公共点,请直接写出t的取值范围.

▼优质解答
答案和解析
(1)如图1中,设点D出发t秒后四边形DFCE的面积为20cm2,根据题意得,
DE=AD=2t,BD=12-2t,CF=DE=2t,
又∵BD×CF=四边形DFCE的面积,
∴2t(12-2t)=20,
t2-6t+5=0,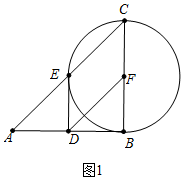
(t-1)(t-5)=0,
解得t1=1,t2=5;
答:点D出发1秒或5秒后四边形DFCE的面积为20cm2.
(2)可能是菱形.
理由:如图1中,∵DE∥CF,DF∥EC,
∴四边形DECF是平行四边形,
∴当DE=DF时,四边形DECF是菱形.
∵△ADE,△DFB都是等腰直角三角形,
∴DE=2t,DF=
(12-2t),
∴2t=
(12-2t),
∴t=12-6
,
答:t=(12-6
)s时,四边形DECF是菱形,
(3)①存在.如图1中,当DB=CF时, F与DE相切.
则有12-2t=2t,
∴t=3,
答:当t=3s时, F与DE相切.
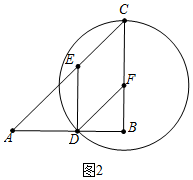
②如图2中,当点D在 F上时, F与四边形DECF有两个公共点,
在Rt△DFB中,∵∠B=90°,AD=DF=CF=2t,BD=BF=12-2t,
∴2t=
(12-2t),
∴t=12-6
,
由图象可知,当12-6
≤t≤6时, F与四边形DFCE至多有两个公共点.
DE=AD=2t,BD=12-2t,CF=DE=2t,
又∵BD×CF=四边形DFCE的面积,
∴2t(12-2t)=20,
t2-6t+5=0,

(t-1)(t-5)=0,
解得t1=1,t2=5;
答:点D出发1秒或5秒后四边形DFCE的面积为20cm2.
(2)可能是菱形.
理由:如图1中,∵DE∥CF,DF∥EC,
∴四边形DECF是平行四边形,
∴当DE=DF时,四边形DECF是菱形.
∵△ADE,△DFB都是等腰直角三角形,
∴DE=2t,DF=
| 2 |
∴2t=
| 2 |
∴t=12-6
| 2 |
答:t=(12-6
| 2 |

(3)①存在.如图1中,当DB=CF时, F与DE相切.
则有12-2t=2t,
∴t=3,
答:当t=3s时, F与DE相切.
②如图2中,当点D在 F上时, F与四边形DECF有两个公共点,
在Rt△DFB中,∵∠B=90°,AD=DF=CF=2t,BD=BF=12-2t,
∴2t=
| 2 |
∴t=12-6
| 2 |
由图象可知,当12-6
| 2 |
看了在Rt△ABC中,∠B=90°...的网友还看了以下:
杠杆什么情况下倾斜静止?1杠杆平衡相当于平衡力吗?是不是原来杠杆运动时若突然两边动阻力、力臂乘积相 2020-04-13 …
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之 2020-05-16 …
角MON=90度,矩形ABCD的顶点A,B分别在边OM,ON上,当点BD在边ON上运动时,点A随之 2020-05-16 …
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之 2020-05-16 …
如图,正方形ABCD的边长为1,动点P从A点出发,沿正方形的边按逆时针方向运动,当它的运动路程为2 2020-05-17 …
如图,正方形ABCD边长为1,动点P从A点出发,沿正方形的边按逆时针方向运动,当它的运动路程为20 2020-05-17 …
三边长都是整数的三角形称为整边三角形,请问周长为6的整边三角形有多少个设每根火柴为1,请动手摆一摆 2020-06-10 …
如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点F、A出发向右移动,点P的 2020-07-13 …
英语翻译1边读边做(动作)2边听边做(动作)3看到一个动作时说出单词,词组,或是句子.翻成英语, 2020-07-15 …
(2011•锦州一模)如图1,在Rt△ABC中,∠ACB=90°,∠A=30°,P为BC边上任意一 2020-07-17 …