早教吧作业答案频道 -->数学-->
已知直线AB∥CD.(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是.(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.(3)如图3,点E在
题目详情
已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是___.
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系___.
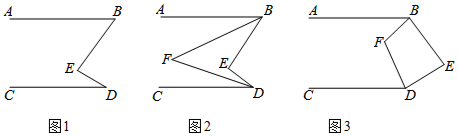
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是___.
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系___.

▼优质解答
答案和解析
 (1)∠ABE+∠CDE=∠BED.
(1)∠ABE+∠CDE=∠BED.
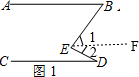
理由:如图1,作EF∥AB,
∵直线AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
故答案为:∠ABE+∠CDE=∠BED.
(2)∠BFD=
∠BED.
理由:如图2,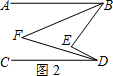 ∵BF,DF分别平分∠ABE,∠CDE,
∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=
∠ABE,∠CDF=
∠CDE,
∴∠ABF+∠CDF=
∠ABE+
∠CDE=
(∠ABE+∠CDE),
由(1),可得∠BFD=∠ABF+∠CDF=
(∠ABE+∠CDE)
∠BED=∠ABE+∠CDE,
∴∠BFD=
∠BED.
(3)2∠BFD+∠BED=360°.
理由:如图3,过点E作EG∥CD,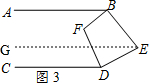 ,
,
∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=
∠ABE,∠CDF=
∠CDE,
∴∠BFD=
(∠ABE+∠CDE),
∴2∠BFD+∠BED=360°.
故答案为:2∠BFD+∠BED=360°.
 (1)∠ABE+∠CDE=∠BED.
(1)∠ABE+∠CDE=∠BED.理由:如图1,作EF∥AB,
∵直线AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
故答案为:∠ABE+∠CDE=∠BED.
(2)∠BFD=
| 1 |
| 2 |
理由:如图2,
 ∵BF,DF分别平分∠ABE,∠CDE,
∵BF,DF分别平分∠ABE,∠CDE,∴∠ABF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABF+∠CDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由(1),可得∠BFD=∠ABF+∠CDF=
| 1 |
| 2 |
∠BED=∠ABE+∠CDE,
∴∠BFD=
| 1 |
| 2 |
(3)2∠BFD+∠BED=360°.
理由:如图3,过点E作EG∥CD,
 ,
,∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BFD=
| 1 |
| 2 |
∴2∠BFD+∠BED=360°.
故答案为:2∠BFD+∠BED=360°.
看了已知直线AB∥CD.(1)如图...的网友还看了以下:
已知abc均为正数学且满足3^a=4^b=6^c则A.1/c=1/a+1/bB.1/c=2/a+2 2020-06-03 …
设f(x)=loga(x-2a)+loga(x-3a),其中a>0且a≠1.(1)已知f(4a)= 2020-06-12 …
1.已知103^a=97^b=1991求1/a+1/b2.已知,a+1/a=2,求a^4+1/a^ 2020-07-12 …
设一种运算程序是x⊕y=a(a为常数),如果(x+1)⊕y=a+1;x⊕(y+1)=a-2.已知1 2020-07-22 …
已知函数f(x)=ax,g(x)=a2x+m,其中m>0,a>0且a≠1.当x∈[-1,1]时,y 2020-07-26 …
1.已知实数a,b,c满足ㄧa-1ㄧ+ㄧb+3ㄧ+ㄧ3c-1ㄧ=0,求(abc)的125次幂除以(a 2020-10-30 …
1.已知y=√x-2-√2-x+5,求y/x的值2.已知√x-2y+1+√2x+y-1=0求x+y的 2020-11-01 …
1.已知a^3+b^3=27,a^2b-ab^2=-6,求代数式(b^3-a^3)+(a^2b-3a 2020-11-01 …
1.已知a-b=5,ab=-9/4,求(1)(a+b)^2的值;(2)a^2+b^2的值.2.已知a 2020-11-05 …
一种用烃A合成高分子化合物N的流程如图:经测定烃A在标准状况下的密度为1.16g•L-1,F和G是同 2020-12-31 …