早教吧作业答案频道 -->数学-->
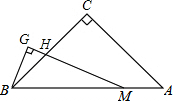
如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=12∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG=cm.
题目详情
如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=
∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG=___cm.
| 1 |
| 2 |

▼优质解答
答案和解析
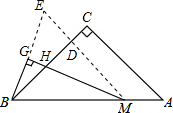 如图,作MD⊥BC于D,延长MD交BG的延长线于E,
如图,作MD⊥BC于D,延长MD交BG的延长线于E,
∵△ABC中,∠C=90°,CA=CB,
∴∠ABC=∠A=45°,
∵∠GMB=
∠A,
∴∠GMB=
∠A=22.5°,
∵BG⊥MG,
∴∠BGM=90°,
∴∠GBM=90°-22.5°=67.5°,
∴∠GBH=∠EBM-∠ABC=22.5°.
∵MD∥AC,
∴∠BMD=∠A=45°,
∴△BDM为等腰直角三角形
∴BD=DM,
而∠GBH=22.5°,
∴GM平分∠BMD,
而BG⊥MG,
∴BG=EG,即BG=
BE,
∵∠MHD+∠HMD=∠E+∠HMD=90°,
∴∠MHD=∠E,
∵∠GBD=90°-∠E,∠HMD=90°-∠E,
∴∠GBD=∠HMD,
∴在△BED和△MHD中,
,
∴△BED≌△MHD(AAS),
∴BE=MH,
∴BG=
MH=4.
故答案是:4.
 如图,作MD⊥BC于D,延长MD交BG的延长线于E,
如图,作MD⊥BC于D,延长MD交BG的延长线于E,∵△ABC中,∠C=90°,CA=CB,
∴∠ABC=∠A=45°,
∵∠GMB=
| 1 |
| 2 |
∴∠GMB=
| 1 |
| 2 |
∵BG⊥MG,
∴∠BGM=90°,
∴∠GBM=90°-22.5°=67.5°,
∴∠GBH=∠EBM-∠ABC=22.5°.
∵MD∥AC,
∴∠BMD=∠A=45°,
∴△BDM为等腰直角三角形
∴BD=DM,
而∠GBH=22.5°,
∴GM平分∠BMD,
而BG⊥MG,
∴BG=EG,即BG=
| 1 |
| 2 |
∵∠MHD+∠HMD=∠E+∠HMD=90°,
∴∠MHD=∠E,
∵∠GBD=90°-∠E,∠HMD=90°-∠E,
∴∠GBD=∠HMD,
∴在△BED和△MHD中,
|
∴△BED≌△MHD(AAS),
∴BE=MH,
∴BG=
| 1 |
| 2 |
故答案是:4.
看了如图,△ABC中,∠C=90°...的网友还看了以下:
一道高二化学题,关于盖斯定律.谢谢!工业制氢气的一个重要反应是:CO(g)+H2O(g)==CO2 2020-04-26 …
下列热化学方程式中,△H能正确表示物质的燃烧热的是A.CO(g)+1/2O2(g)==CO2(g) 2020-05-13 …
已知A基因含23000个碱基对,其中一条链A:C:T:G=1:2:3:4,连续复制3次,至少需要G 2020-05-23 …
已知函数f(x-1)的图像与函数g(x)的图像关于直线y=x对称,且g(1)=2则:A,f(1)= 2020-06-27 …
已知A(g)+B(g)⇌C(g)+D(g)反应的平衡常数和温度的关系如下:|温度/℃7009008 2020-07-05 …
炽热的炉膛内有反应:C(s)+O2(g)CO2(g)ΔH=-392kJ·mol-1,往炉膛内通入水 2020-07-19 …
若f(x),g(x)的定义域都是R,且x-f(g(x)=0有实数解,则g(f(x))不可能是()A 2020-07-31 …
f(x)=ax-lnx,g(x)=b/x+clnx(a,b,c为非零常数)1,若y=1是曲线f(x) 2020-11-06 …
碱基计算的规律.①A等于T,G等于C,A+G=T+CA+G/T+C等1.②一条单链的A+G/T+C的 2020-11-27 …
已知砼配比为C:S:G=1:2.4:4,w/c=0.6.表观密度为2420kg/m3.求材料用量.麻 2021-02-01 …