如图所示，竖直平面内光滑圆轨道半径R=2m，从最低点A有一质量为m=1kg的小球开始运动，初速度v0方向水平向右，重力加速度g取10m/s2，下列说法正确的是（）A.小球能到达最高点B的条件

Question

如图所示，竖直平面内光滑圆轨道半径R=2m，从最低点A有一质量为m=1kg的小球开始运动，初速度v₀方向水平向右，重力加速度g取10m/s²，下列说法正确的是（　　）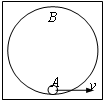

A. 小球能到达最高点B的条件是v₀≥4

√(5)m/s

B. 若初速度v₀=5m/s，则运动过程中，小球一定不会脱离圆轨道

C. 若初速度v₀=8m/s，则小球将在离A点3.2m高的位置离开圆轨道

D. 若初速度v₀=8m/s，则小球离开圆轨道时的速度大小为2

√(2)m/s

Answer 1

A、当小球能到达最高点时，由重力提供向心力，此时速度最小，则
mg=m(v2)/(R)
解得：v=√(gR)=√(20)m/s
从A到B的过程中，根据动能定理得：
(1)/(2)mv2-(1)/(2)mv02=-mg•2R
解得：v₀=10m/s
所以小球能到达最高点B的条件是v₀≥10m/s，故A错误；
B、当小球恰好运动到AB中点时，有 mgR=(1)/(2)m

v

2 0

，v₀=√(2gR)=√(2×10×2)=2√(10)m/s>5m/s．则小球在轨道下部分来回运动，一定不会离开轨道，故B正确；
C、刚好脱离轨道时，轨道对小球的弹力为零，重力沿半径方向的分量提供向心力，设此时重力方向与半径方向的夹角为θ，则
mgcosθ=m(v′2)/(R)
根据几何关系得：cosθ=(h)/(R)
根据动能定理得：(1)/(2)mv′2-(1)/(2)mv02=-mg•(R+h)
解得：v′=2√(2)m/s，h=0.8m
所以离开圆轨道得位置离A点的距离为H=0.8+2=2.8m，故C错误，D正确．
故选：BD