早教吧作业答案频道 -->数学-->
如图,正方形ABCD的边长为4,点P为对角线BD上一动点,点E在射线BC上.(1)填空:∠PBC=度.(2)若BE=t,连结PE、PC,则|PE+PC的最小值为,|PE-PC|的最大值是(用含t的代数式表示);(3
题目详情
如图,正方形ABCD的边长为4,点P为对角线BD上一动点,点E在射线BC上.
(1)填空:∠PBC=___度.
(2)若BE=t,连结PE、PC,则|PE+PC的最小值为___,|PE-PC|的最大值是___(用含t的代数式表示);
(3)若点E 是直线AP与射线BC的交点,当△PCE为等腰三角形时,求∠PEC的度数.
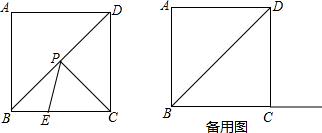
(1)填空:∠PBC=___度.
(2)若BE=t,连结PE、PC,则|PE+PC的最小值为___,|PE-PC|的最大值是___(用含t的代数式表示);
(3)若点E 是直线AP与射线BC的交点,当△PCE为等腰三角形时,求∠PEC的度数.

▼优质解答
答案和解析
(1)∠PBC=45度;
故答案为:45;
(2)如图1所示:当AP与PE在一条线上时,PE+PC最小,
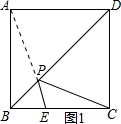
∵AB=4,BE=t,
∴PE+PC的最小值为
;
当P与B重合时,|PE-PC|的最大值,最大值是|4-t|;
故答案为:
;|4-t|;
(3)分两种情况考虑:
①当点E在BC的延长线上时,
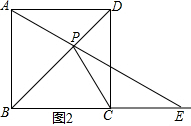
如图2所示,△PCE是等腰三角形,则CP=CE,
∴∠CPE=∠CEP,
∴∠BCP=∠CPE+∠CEP=2∠CEP,
∵在正方形ABCD中,∠ABC=90°,
∴∠PBA=∠PBC=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=2∠CEP,
∵∠BAP+∠PEC=90°,
∴2∠PEC+∠PEC=90°,
∴∠PEC=30°;
②当点E在BC上时,
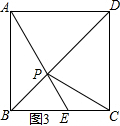
如图3所示,△PCE是等腰三角形,则PE=CE,
∴∠CPE=∠PCE,
∴∠BEP=∠CPE+∠PCE=2∠ECP,
∵四边形ABCD是正方形,
∴∠PBA=∠PBC=45°,
又AB=BC,BP=BP,
∴△ABP≌△CBP,
∴∠BAP=∠BCP,
∵∠BAP+∠AEB=90°,
∴2∠BCP+∠BCP=90°,
∴∠BCP=30°,
∴∠AEB=60°,
∴∠PEC=180°-∠AEB=120°,
综上所述:当△PCE为等腰三角形时,∠PEC的度数为30°或120°.
故答案为:45;
(2)如图1所示:当AP与PE在一条线上时,PE+PC最小,

∵AB=4,BE=t,
∴PE+PC的最小值为
| 16+t2 |
当P与B重合时,|PE-PC|的最大值,最大值是|4-t|;
故答案为:
| 16+t2 |
(3)分两种情况考虑:
①当点E在BC的延长线上时,

如图2所示,△PCE是等腰三角形,则CP=CE,
∴∠CPE=∠CEP,
∴∠BCP=∠CPE+∠CEP=2∠CEP,
∵在正方形ABCD中,∠ABC=90°,
∴∠PBA=∠PBC=45°,
在△ABP和△CBP中,
|
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=2∠CEP,
∵∠BAP+∠PEC=90°,
∴2∠PEC+∠PEC=90°,
∴∠PEC=30°;
②当点E在BC上时,

如图3所示,△PCE是等腰三角形,则PE=CE,
∴∠CPE=∠PCE,
∴∠BEP=∠CPE+∠PCE=2∠ECP,
∵四边形ABCD是正方形,
∴∠PBA=∠PBC=45°,
又AB=BC,BP=BP,
∴△ABP≌△CBP,
∴∠BAP=∠BCP,
∵∠BAP+∠AEB=90°,
∴2∠BCP+∠BCP=90°,
∴∠BCP=30°,
∴∠AEB=60°,
∴∠PEC=180°-∠AEB=120°,
综上所述:当△PCE为等腰三角形时,∠PEC的度数为30°或120°.
看了如图,正方形ABCD的边长为4...的网友还看了以下:
已知字母组合成英语单词1、e e t t i n h r 2、e e r a t w h 3、o 2020-05-14 …
考查下列文法:C(VT,VN,E,P) 其中:VT={+,*,(,),i} VN={E,T,F} E 2020-05-26 …
考查文法:G(VT,VN,E,P) 其中,VT={+,*,(,),i},VN={E,T,F},E为开 2020-05-26 …
重新排列字母,写出单词1.s,a,p,e,c,2.r,o,e,t,c,k,3.d,c,o,o,t, 2020-06-06 …
tr--e-,t--el,---c-me.这三个单词分别是什么.横线上填英语字母 2020-06-07 …
英语单词填空1.时间状语:d-r-n-2.场所:b-s-s-o-f-r--e-a-t-e-t3.教 2020-07-14 …
用r,e,t,a,c,l,v,i,h拼出单词(6-10个)不一定要用全部,只要用到其中几个就可以了1 2020-11-01 …
已知文法G:(1)E→E+T|T(2)T→T*F|F(3)F→P↑F|P(4)P→(E)|i1.已知 2020-12-07 …
英语:下1.将下联打乱的字母组成单词,并写出汉语意思1.a,e,h,g,c,n[]2.e,i,s,t 2020-12-10 …
英文单词分类填空动物类1.O()t()p()s2.k()t()e()3.l()b()t()r4.a( 2021-02-05 …