早教吧作业答案频道 -->数学-->
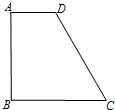
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,∠BCD=60°,CD=5.将梯形ABCD绕点A旋转后得到梯形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,当点B1落在边CD上时,点D1恰好落在CD的延长线上,
题目详情
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,∠BCD=60°,CD=5.将梯形ABCD绕点A旋转后得到梯形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,当点B1落在边CD上时,点D1恰好落在CD的延长线上,那么DD1的长为___.

▼优质解答
答案和解析
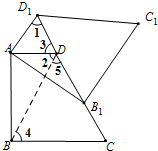 如图,将梯形ABCD绕点A旋转后得到梯形AB1C1D1,连接BD,
如图,将梯形ABCD绕点A旋转后得到梯形AB1C1D1,连接BD,
由旋转得:AD=AD1,AB=AB1,∠DAD1=∠BAB1,
∴∠DAB=∠D1AB1,且∠1=∠3,
在△DAB和△D1AB1中,
,
∴△DAB≌△D1AB1(SAS),
∴∠1=∠2,
∴∠2=∠3,
∵AD∥BC,
∴∠2=∠4,
设∠1=∠2=∠3=∠4=α,则∠5=180°-∠4-∠C=120°-α,
∵∠2+∠3+∠5=180°,
∴α+α+120°-α=180°,
解得α=60°,
∴∠1=∠2=∠3=∠4=60°,
∴△ADD1、△BCD都是等边三角形,
∴BD=CD=5,∠ABD=30°,
∴Rt△ABD中,AD=
BD=
,
∴DD1=AD=
.
故答案为:
 如图,将梯形ABCD绕点A旋转后得到梯形AB1C1D1,连接BD,
如图,将梯形ABCD绕点A旋转后得到梯形AB1C1D1,连接BD,由旋转得:AD=AD1,AB=AB1,∠DAD1=∠BAB1,
∴∠DAB=∠D1AB1,且∠1=∠3,
在△DAB和△D1AB1中,
|
∴△DAB≌△D1AB1(SAS),
∴∠1=∠2,
∴∠2=∠3,
∵AD∥BC,
∴∠2=∠4,
设∠1=∠2=∠3=∠4=α,则∠5=180°-∠4-∠C=120°-α,
∵∠2+∠3+∠5=180°,
∴α+α+120°-α=180°,
解得α=60°,
∴∠1=∠2=∠3=∠4=60°,
∴△ADD1、△BCD都是等边三角形,
∴BD=CD=5,∠ABD=30°,
∴Rt△ABD中,AD=
| 1 |
| 2 |
| 5 |
| 2 |
∴DD1=AD=
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
看了如图,在直角梯形ABCD中,A...的网友还看了以下:
下列命题中错误的命题为()A、圆既是轴对称图形,也是中心对称图形B、长度相等的弧是等弧C、三角形的 2020-07-30 …
5、下列命题中,正确的是()A、正多边形都是轴对称图形B、正多边形都是中心对称图形C、每个内角都相 2020-08-01 …
关于等边三角形,下列说法不正确的是()A.等边三角形是轴对称图形B.所有的等边三角形都相似C.等边 2020-08-03 …
下列图形中,是轴对称图形而不是中心对称图形的是()A.矩形B.菱形C.正方形D.等腰梯形 2020-08-03 …
(2006•河北区一模)下列图形中,是轴对称图形而不是中心对称图形的是()A.矩形B.菱形C.正方 2020-08-03 …
下列平面图形,既是中心对称图形,又是轴对称图形的是()A.等腰三角形B.正五边形C.平行四边形D. 2020-08-03 …
等边三角形、矩形、菱形和圆中,既是轴对称图形,又是中心对称图形的是()A.等边三角形和圆B.等边三 2020-08-03 …
自行车车轮要做成圆形,实际上是根据圆的特征()A.圆是轴对称图形B.直径是圆中最长的弦C.圆上各点 2020-08-03 …
矩形是轴对称图形,下列说发正确的是A矩形有两条对称轴,这两条对称轴是它的对角线B矩形有一条对称轴, 2020-08-03 …
下列条件中,不能得到等边三角形的是()A.有两个内角是60°的三角形B.有两边相等且是轴对称图形的三 2020-11-11 …