已知函数f（x）=（x-2）ex+ax（a∈R）（1）试确定函数f（x）的零点个数；（2）设x1，x2是函数f（x）的两个零点，当x1+x2≤2时，求a的取值范围．

Question

已知函数f（x）=（x-2）e^x+ax（a∈R）
（1）试确定函数f（x）的零点个数；
（2）设x₁，x₂是函数f（x）的两个零点，当x₁+x₂≤2时，求a的取值范围．

Answer 1

（1）由f（x）=（x-2）e^x+ax=0得ax=（2-x）e^x，
令g（x）=（2-x）e^x，则g′（x）=-e^x+（2-x）e^x=（1-x）e^x，
∴当x>1时，g′（x）<0，当x<1时，g′（x）>0，
∴g（x）在（-∞，1）上单调递增，在（1，+∞）上单调递减，
∴当x=1时，函数g（x）有最大值g（1）=e，
又当x<1时，g（x）=（2-x）e^x>0，g（2）=0；
作出y=g（x）与y=ax的函数图象如图所示：

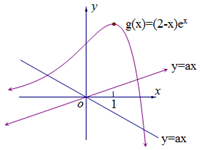
∴当a≥0时，y=ax与g（x）只有一个公共点，从而函数f（x）有一个零点；
当a<0时，y=ax与g（x）有两个公共点，从而函数f（x）有两个零点．
（II）设x₁2，由（I）知a<0且x₁<0，x₂>2，
由f（x₁）=（x₁-2）e x1+ax₁=0，得a=((2-x1)ex1)/(x1)（x₁<0），
由f（x₂）=（x₂-2）e x2+ax₂=0，得a=((2-x2)ex2)/(x2)（x₂>2）．
∴a²=([x1x2-2(x1+x2)+4]ex1+x2)/(x1x2)，
∵x₁+x₂≤2，∴4-2（x₁+x₂）≥0，0<e x1+x2≤e²，（当且仅当x₁+x₂=2时取等号）
∴4-2（x₁+x₂）+x₁x₂≥x₁x₂，又x₁x₂<0，
∴(x1x2-2(x1+x2)+4)/(x1x2)≤1，
∴a²≤e x1+x2≤e²，
又a<0，∴-e≤a<0．